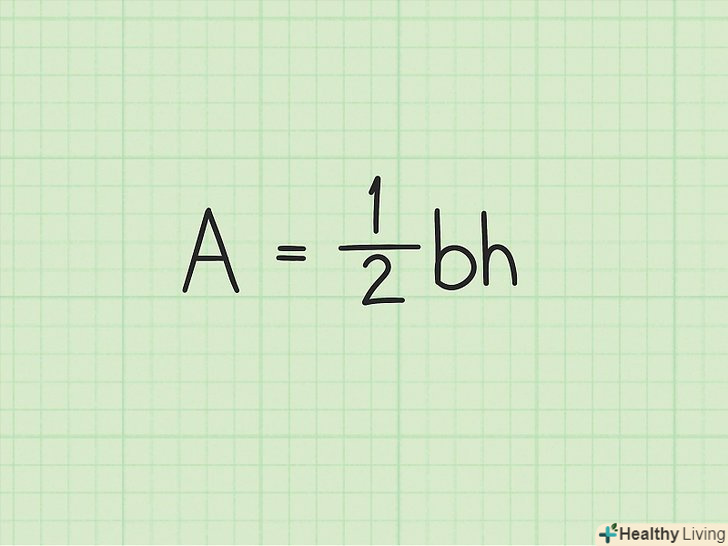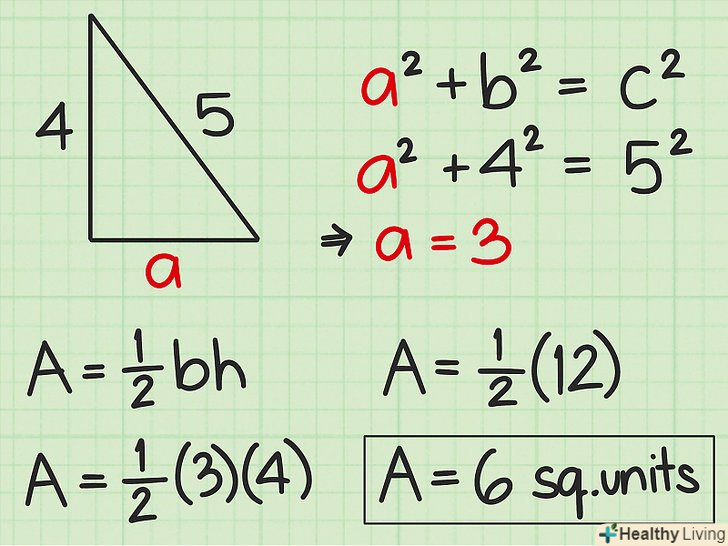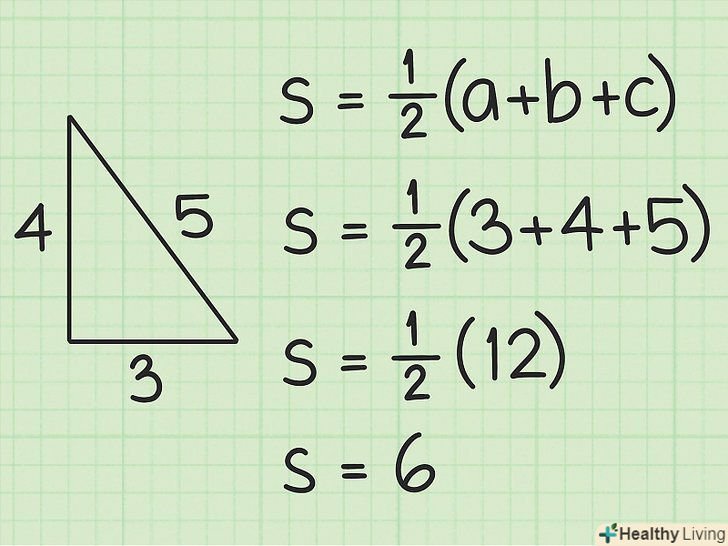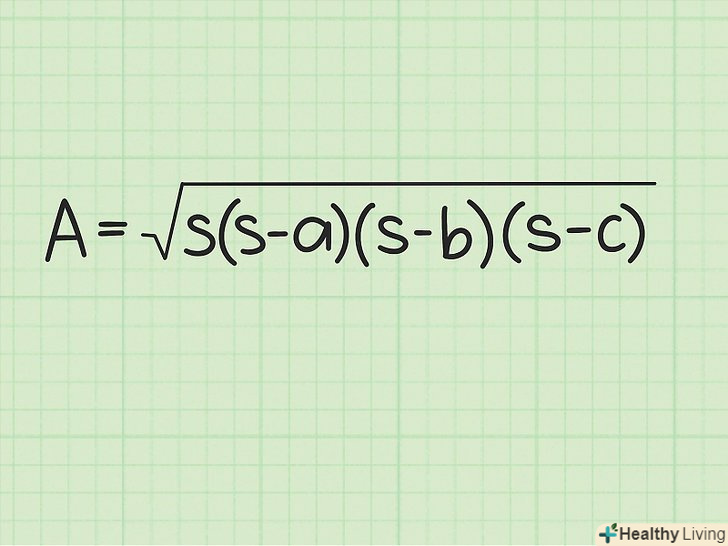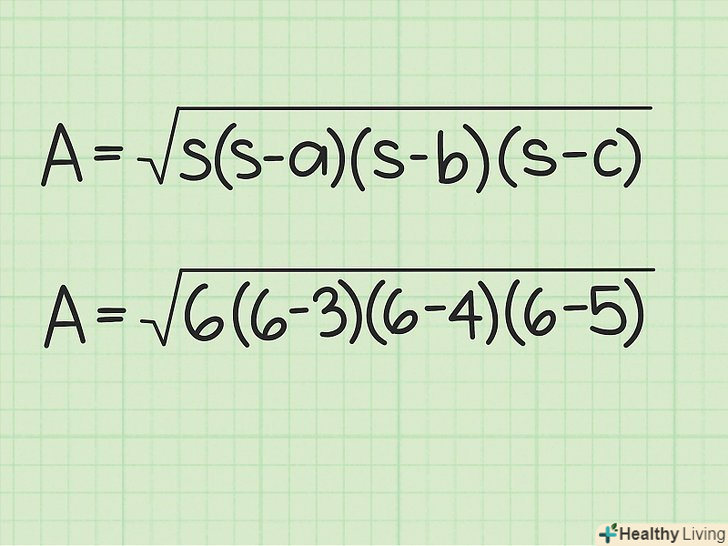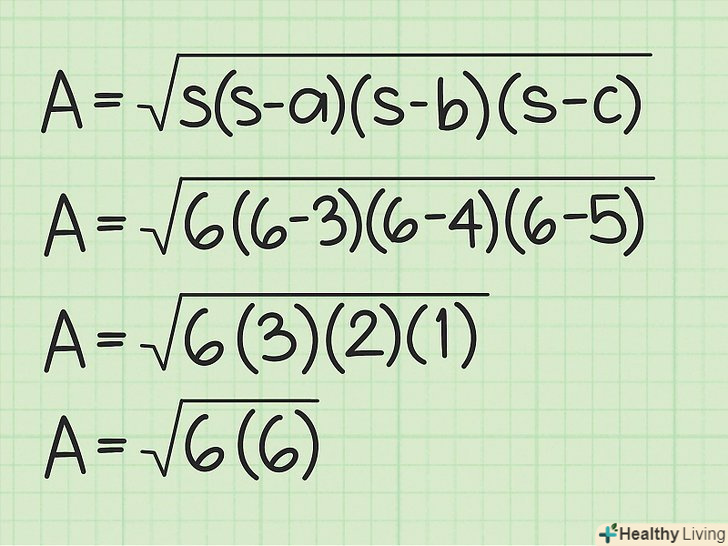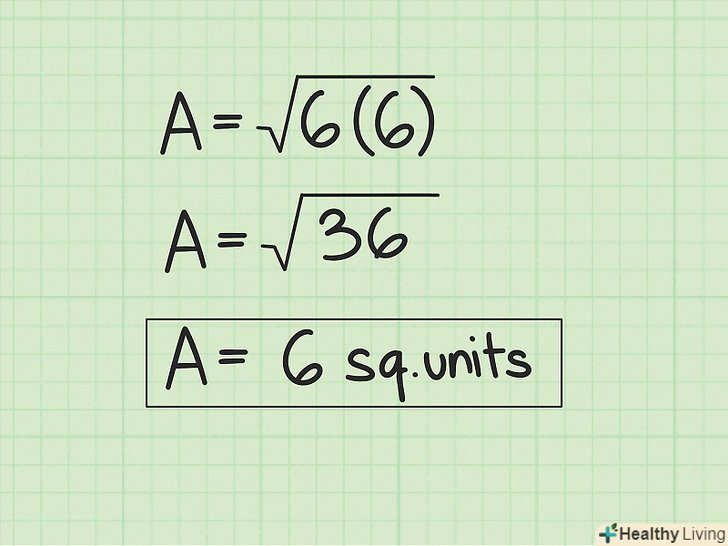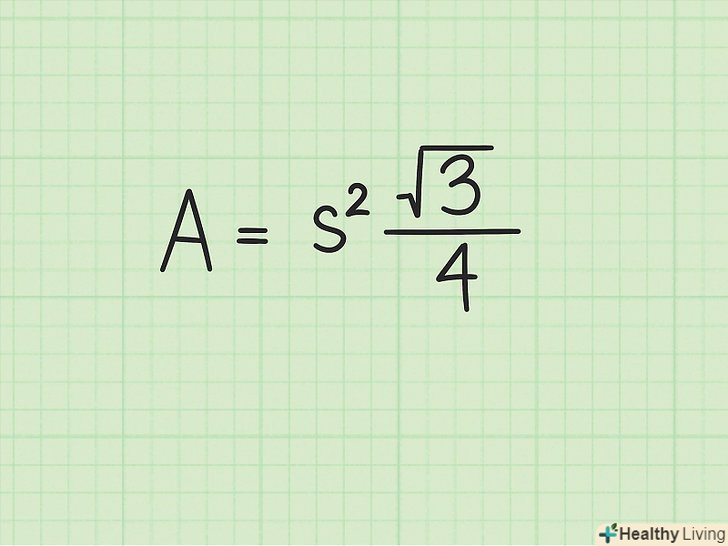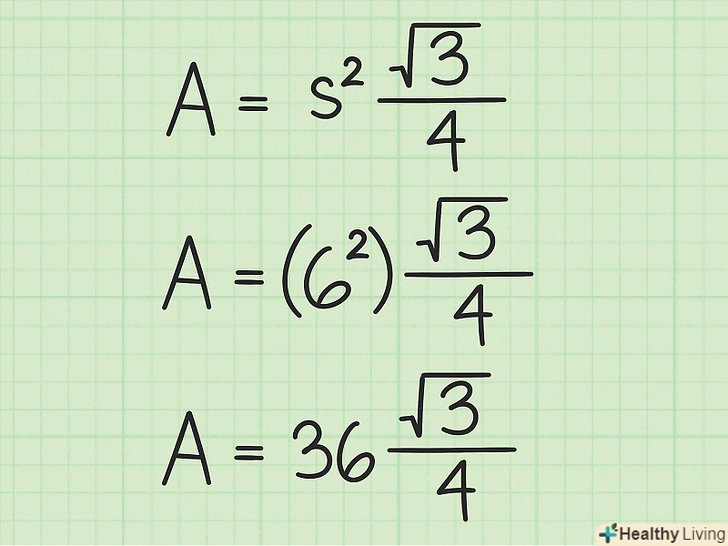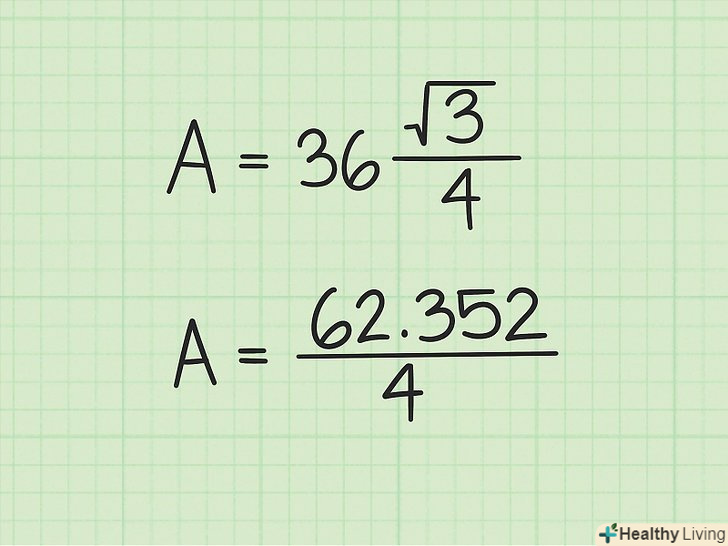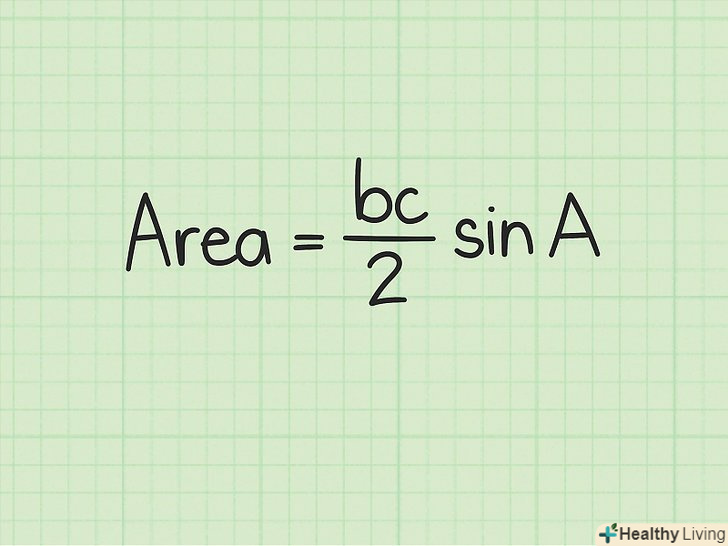Найпоширеніший спосіб обчислити площу трикутника - це розділити навпіл результат перемноження висоти і підстави. Але існують і інші формули для обчислення площі трикутника, які застосовуються в залежності від даних значень. Також можна знайти площу трикутника по відомих сторонах і кутах трикутника (тобто без використання висоти).
Кроки
Метод1З 4:
По підставі і висоті
Метод1З 4:
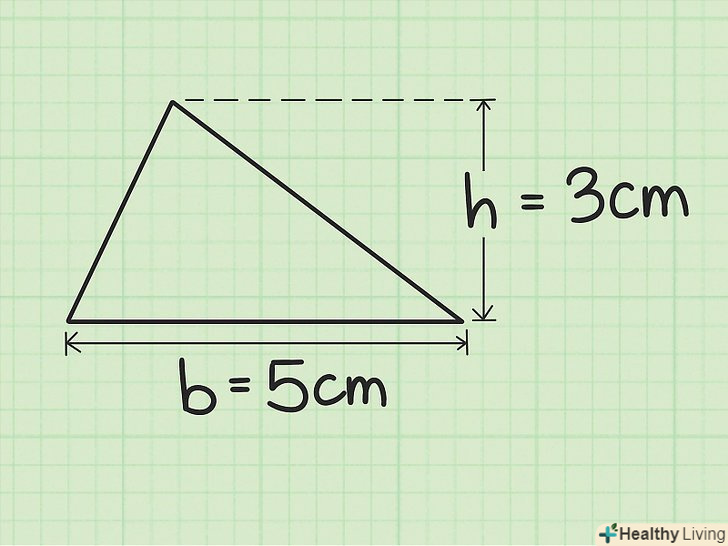
 Знайдіть основу і висоту трикутника.підстава-це одна зі сторін трикутника. Висота - це перпендикуляр, проведений до основи з протилежної вершини трикутника. Значення основи і висоти будуть дані в задачі або потрібно виміряти їх.
Знайдіть основу і висоту трикутника.підстава-це одна зі сторін трикутника. Висота - це перпендикуляр, проведений до основи з протилежної вершини трикутника. Значення основи і висоти будуть дані в задачі або потрібно виміряти їх.- Наприклад, дано трикутник з основою 5 см і висотою 3 см.
 Запишіть формулу для обчислення площі трикутника. Формула:
Запишіть формулу для обчислення площі трикутника. Формула:, де
— підстава,
— висота.[1] зверніть увагу: тут і далі на малюнках площа позначена як
, але в формулах використовується
.
 Підставте значення підстави і висоти в формулу. перемножте ці значення, а потім розділіть їх на 2 (або помножте на
Підставте значення підстави і висоти в формулу. перемножте ці значення, а потім розділіть їх на 2 (або помножте на). Ви отримаєте площу трикутника (в квадратних одиницях виміру).
- Наприклад, якщо основа трикутника дорівнює 5 см, а висота дорівнює 3 см, то обчислення виглядають так:
Таким чином, площа трикутника з основою 5 см і висотою 3 см дорівнює 7,5 квадратних сантиметрів.
- Наприклад, якщо основа трикутника дорівнює 5 см, а висота дорівнює 3 см, то обчислення виглядають так:
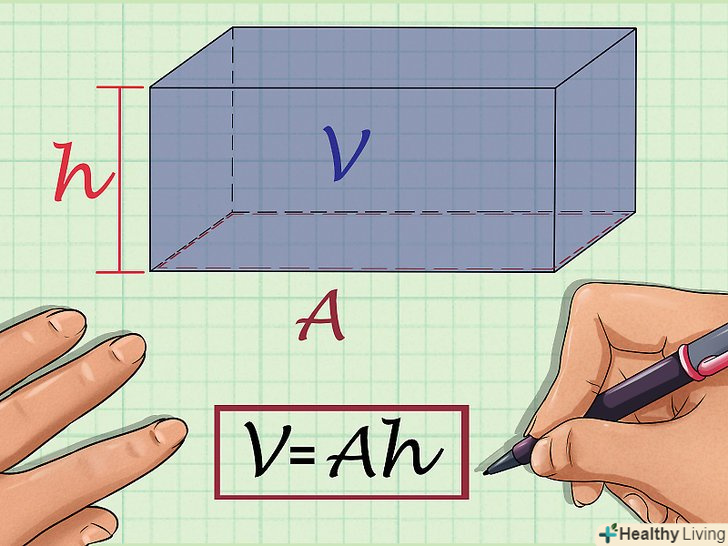
 Знайдіть площу прямокутного трикутника.Так як дві сторони (катети) прямокутного трикутника перпендикулярні, один з катетів є висотою, а другий — підставою. Таким чином, якщо значення підстави і висоти в задачі не дані, можна визначити їх по довжинах сторін трикутника. Площа трикутника обчислюється за формулою:
Знайдіть площу прямокутного трикутника.Так як дві сторони (катети) прямокутного трикутника перпендикулярні, один з катетів є висотою, а другий — підставою. Таким чином, якщо значення підстави і висоти в задачі не дані, можна визначити їх по довжинах сторін трикутника. Площа трикутника обчислюється за формулою:- Також можна користуватися цією формулою, якщо відомий тільки один катет і гіпотенуза. Гіпотенуза-це сторона прямокутного трикутника, протилежна прямому куту. Пам'ятайте, що невідому сторону прямокутного трикутника можна знайти Потеоремі Піфагора:
.
- Наприклад, якщо позначити гіпотенузу як "с«, то катети позначаються як» a «і»b". Якщо гіпотенуза дорівнює 5 см, а підстава (один з катетів) дорівнює 4 см, за теоремою Піфагора можна знайти висоту (інший катет):
Тепер у формулу для обчислення площі замість b і h підставте значення двох катетів (a і b):
- Також можна користуватися цією формулою, якщо відомий тільки один катет і гіпотенуза. Гіпотенуза-це сторона прямокутного трикутника, протилежна прямому куту. Пам'ятайте, що невідому сторону прямокутного трикутника можна знайти Потеоремі Піфагора:
Метод2З 4:
По сторонах
Метод2З 4:
 Обчисліть напівпериметр трикутника.напівпериметр фігури дорівнює половині її периметра. Щоб знайти напівпериметр, спочатку потрібно обчислити периметр трикутника, тобто скласти значення трьох сторін, а потім периметр розділити на 2 (або помножити на
Обчисліть напівпериметр трикутника.напівпериметр фігури дорівнює половині її периметра. Щоб знайти напівпериметр, спочатку потрібно обчислити периметр трикутника, тобто скласти значення трьох сторін, а потім периметр розділити на 2 (або помножити на).[2] зверніть увагу: тут і далі на малюнках напівпериметр позначений як
, але в формулах використовується
.
- Наприклад, дано трикутник, сторони якого рівні 5 см, 4 см і 3 см. Напівпериметр обчислюється так:
- Наприклад, дано трикутник, сторони якого рівні 5 см, 4 см і 3 см. Напівпериметр обчислюється так:

 Підставте значення напівпериметра і сторін в формулу. напівпериметр підставляється замість
Підставте значення напівпериметра і сторін в формулу. напівпериметр підставляється замість.
- У нашому прикладі:
- У нашому прикладі:
 Обчисліть вирази в дужках. відніміть значення кожної сторони з значення напівпериметра. Потім перемножте отримані результати.
Обчисліть вирази в дужках. відніміть значення кожної сторони з значення напівпериметра. Потім перемножте отримані результати.- У нашому прикладі:
- У нашому прикладі:
 Перемножте значення, що стоять під знаком кореня.потім з отриманого результату витягніть квадратний корінь. Ви отримаєте площу трикутника (в квадратних одиницях виміру).
Перемножте значення, що стоять під знаком кореня.потім з отриманого результату витягніть квадратний корінь. Ви отримаєте площу трикутника (в квадратних одиницях виміру).- У нашому прикладі:
Таким чином, площа трикутника дорівнює 6 квадратних сантиметрів.
- У нашому прикладі:
Метод3З 4:
По одній зі сторін рівностороннього трикутника
Метод3З 4:
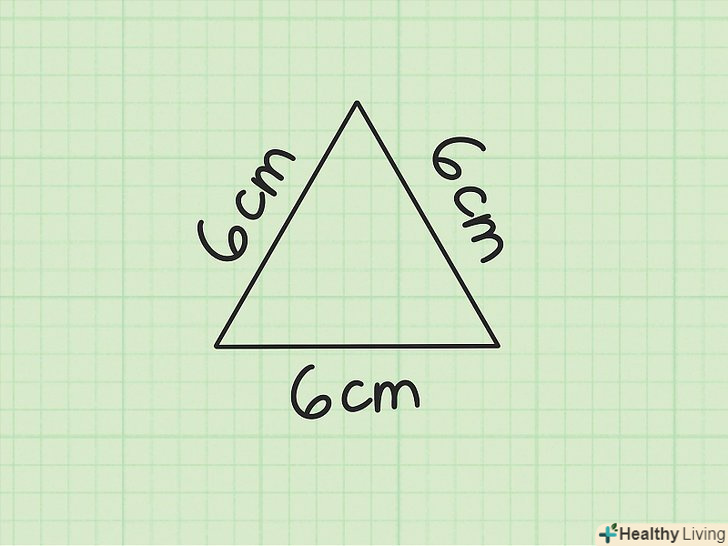
 Знайдіть довжину однієї сторони трикутника. у рівносторонньому трикутнику всі сторони і всі кути рівні, тому досить знати значення тільки однієї сторони.[4]
Знайдіть довжину однієї сторони трикутника. у рівносторонньому трикутнику всі сторони і всі кути рівні, тому досить знати значення тільки однієї сторони.[4]- Наприклад, дано трикутник, всі сторони якого рівні 6 см.
 Запишіть формулу для обчислення площі рівностороннього трикутника. Формула:
Запишіть формулу для обчислення площі рівностороннього трикутника. Формула:, де
— сторона рівностороннього трикутника.[5]
 У формулу підставте значення сторони трикутника. воно підставляється замість
У формулу підставте значення сторони трикутника. воно підставляється замість. Потім зведіть значення в квадрат.
- Наприклад, якщо сторона рівностороннього трикутника дорівнює 6 см, обчислення запишуться так:
- Наприклад, якщо сторона рівностороннього трикутника дорівнює 6 см, обчислення запишуться так:
 Помножте квадрат сторони на
Помножте квадрат сторони на. щоб витягти корінь і отримати точне значення, скористайтеся калькулятором. Якщо калькулятора немає,
≈ 1,732.
- У нашому прикладі:
- У нашому прикладі:
 Результат розділіть на 4.ви отримаєте площу трикутника (в квадратних одиницях виміру).
Результат розділіть на 4.ви отримаєте площу трикутника (в квадратних одиницях виміру).- У нашому прикладі:
Таким чином, площа рівностороннього трикутника, сторони якого дорівнюють 6 см, приблизно дорівнює 15,59 квадратних сантиметрів.
- У нашому прикладі:
Метод4З 4:
За допомогою тригонометричних функцій
Метод4З 4:
 Знайдіть довжини двох суміжних сторін і прилеглий кут.суміжні сторони сходяться в одній вершині трикутника.[6] прилеглий Кут знаходиться між суміжними сторонами.
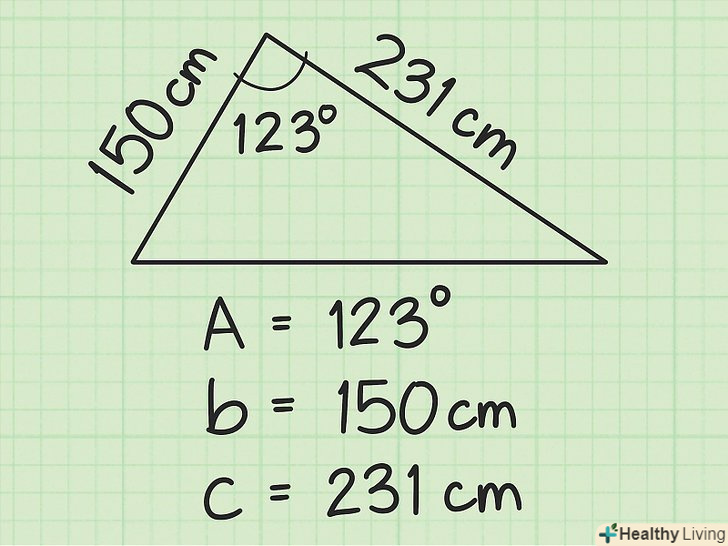
Знайдіть довжини двох суміжних сторін і прилеглий кут.суміжні сторони сходяться в одній вершині трикутника.[6] прилеглий Кут знаходиться між суміжними сторонами.- Наприклад, дано трикутник, суміжні сторони якого рівні 150 см і 231 см, а кут між ними дорівнює 123 градуси.
 Запишіть формулу для обчислення площі трикутника за допомогою тригонометричних функцій. Формула:
Запишіть формулу для обчислення площі трикутника за допомогою тригонометричних функцій. Формула:, де
і
— суміжні сторони,
— кут між ними.[7]
 У формулу підставте значення сторін. вони підставляються замість
У формулу підставте значення сторін. вони підставляються замість