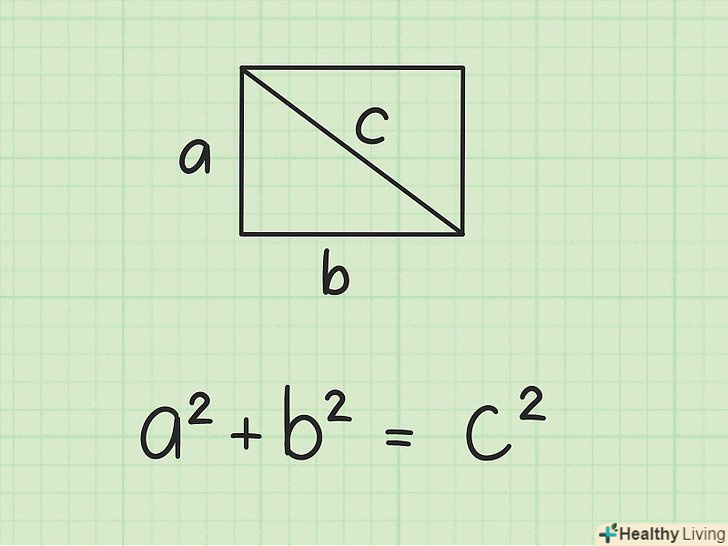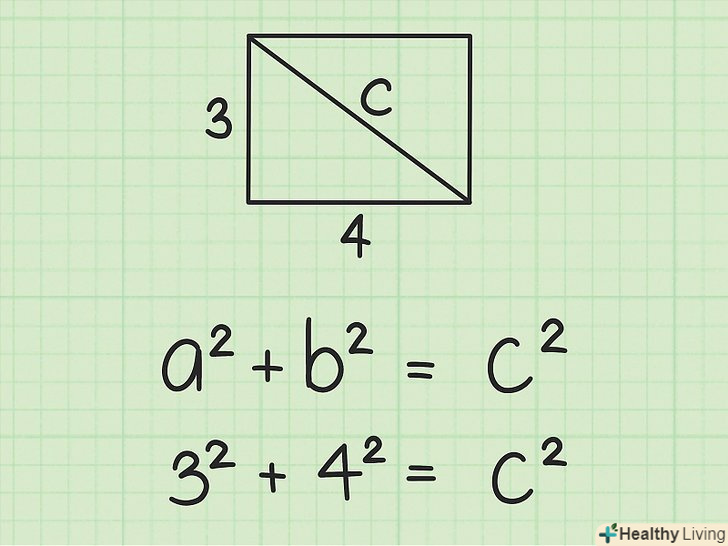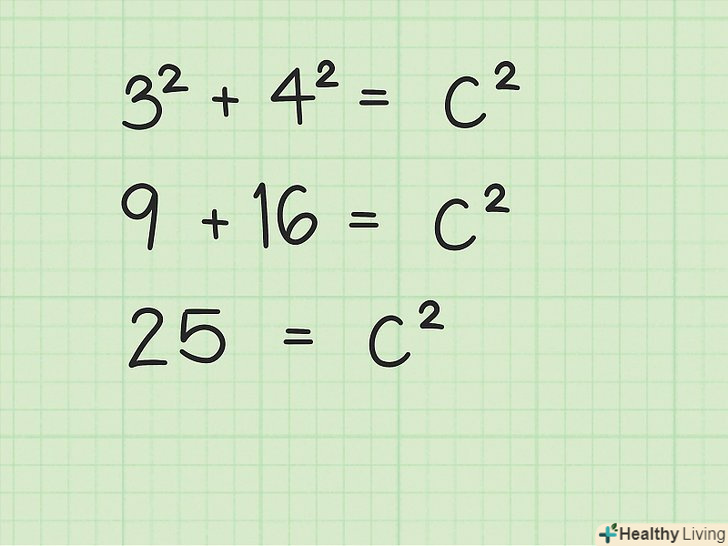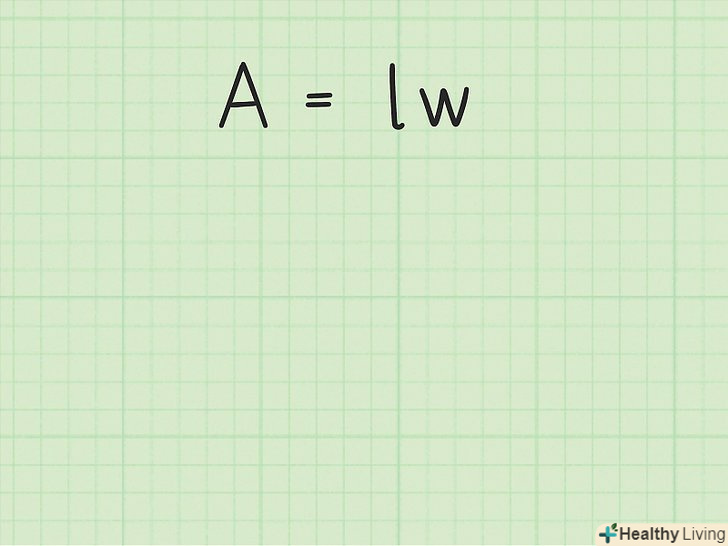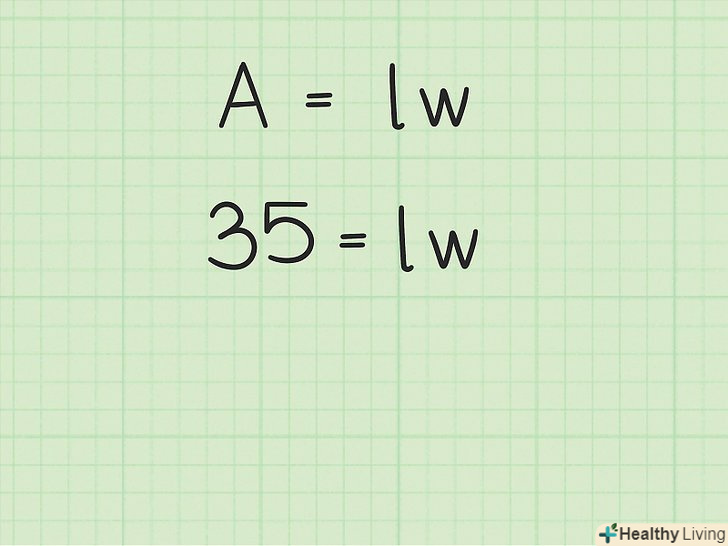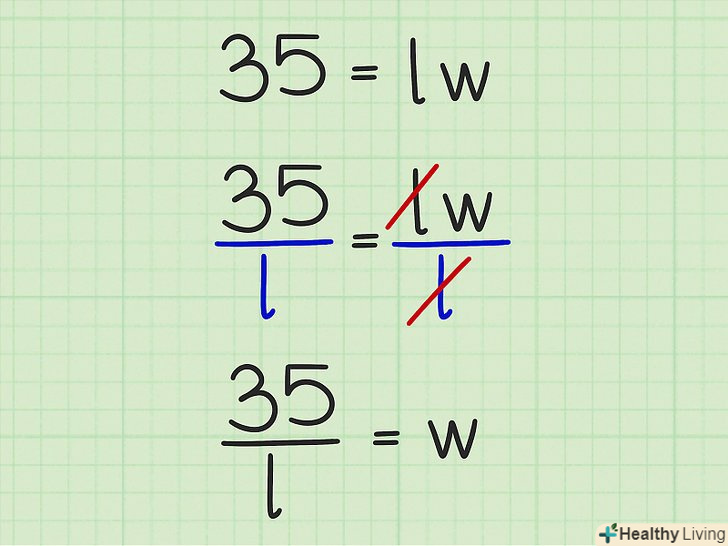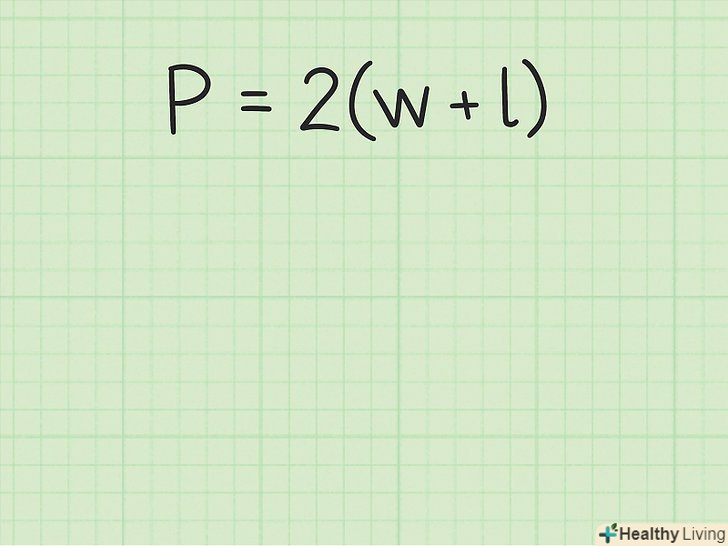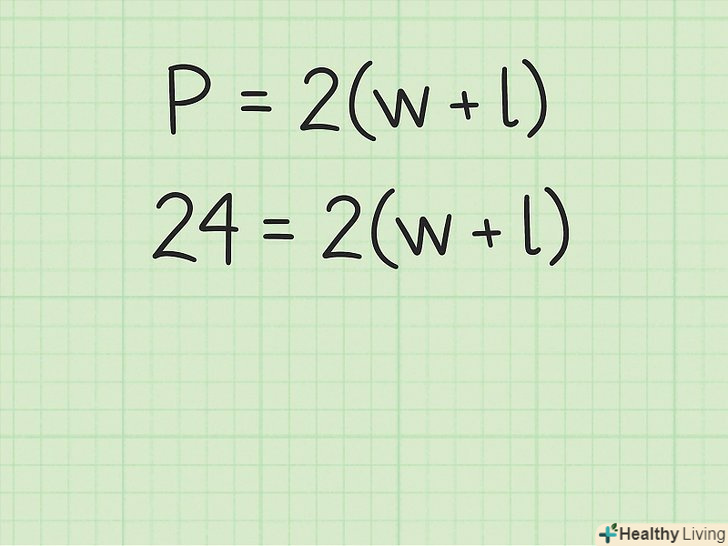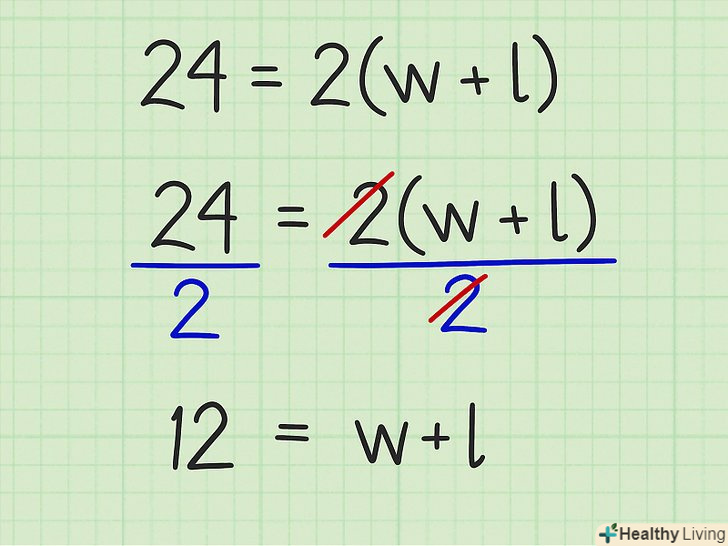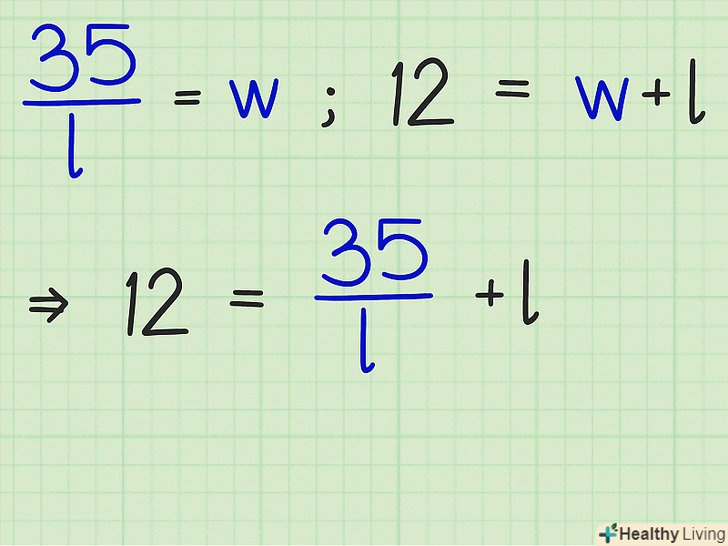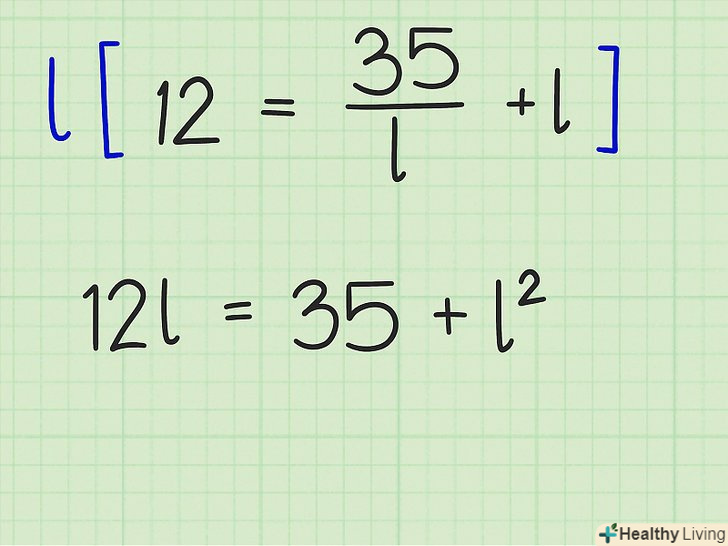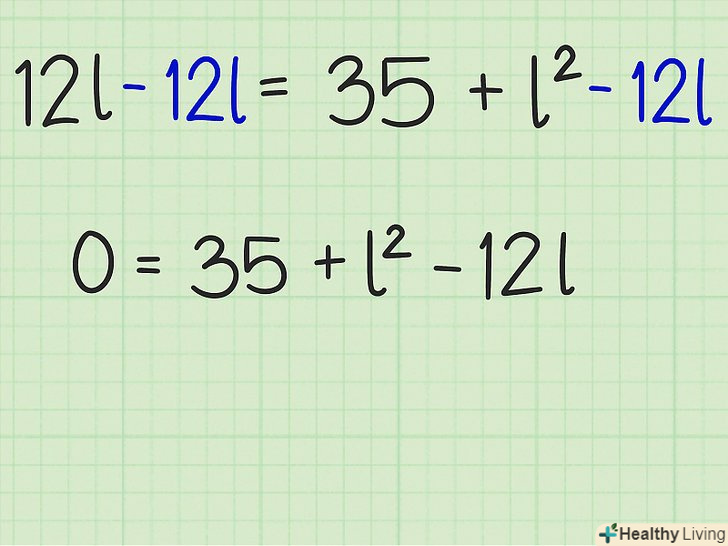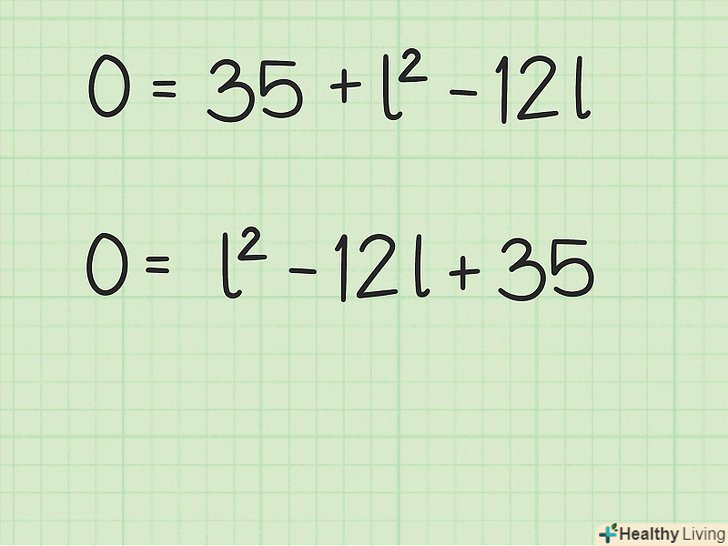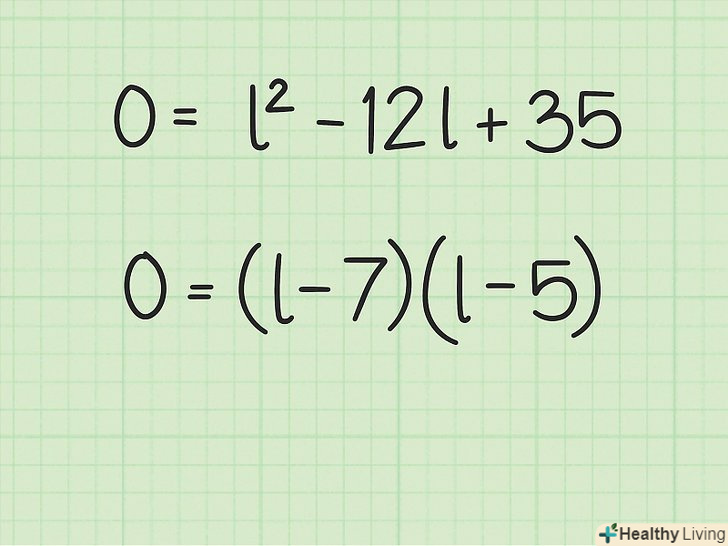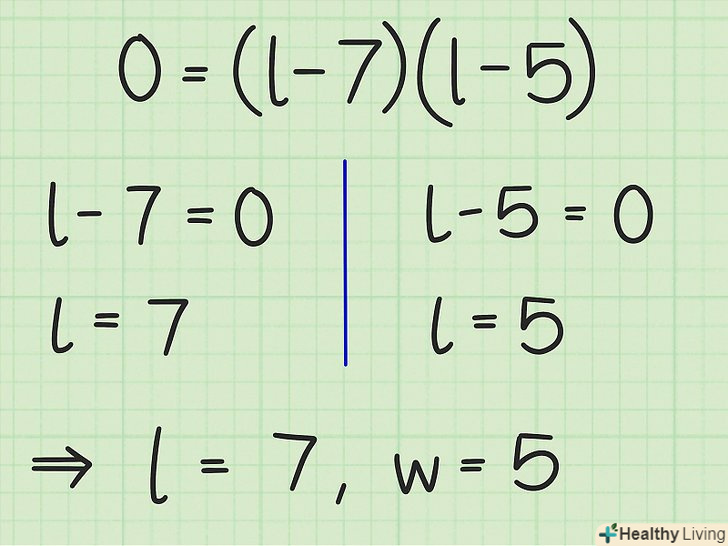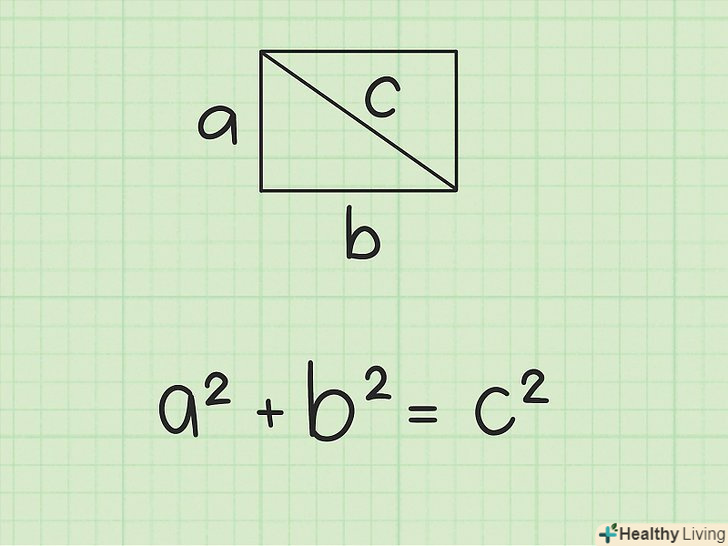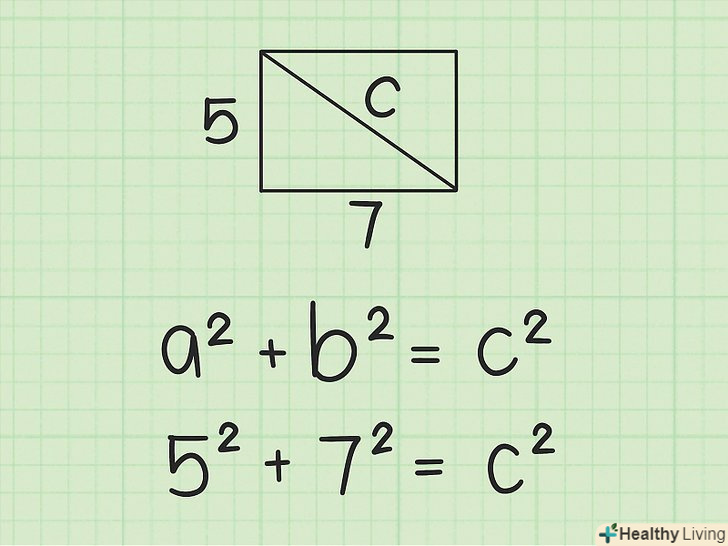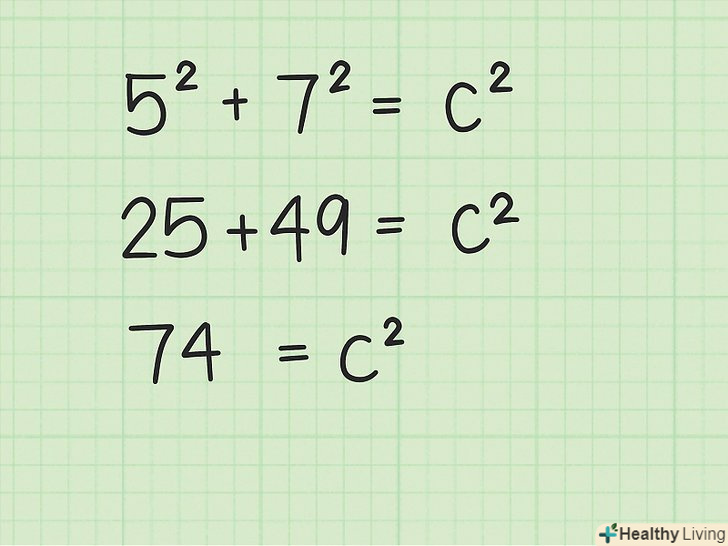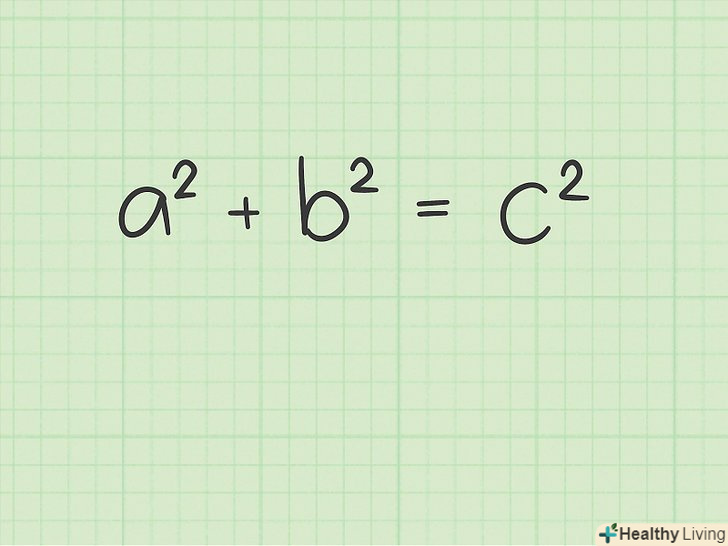Діагональ-це відрізок, який з'єднує дві протилежні вершини прямокутника.[1] у прямокутнику дві рівні діагоналі.[2] якщо відомі сторони прямокутника, діагональ можна знайти по теоремі Піфагора, тому що діагональ ділить прямокутник на два прямокутних трикутника. Якщо сторони не дані, але відомі інші величини, наприклад, площа і периметр або відношення сторін, можна знайти сторони прямокутника, а потім по теоремі Піфагора обчислити діагональ.
Кроки
Метод1З 3:
По сторонах
Метод1З 3:
 Запишіть теорему Піфагора. Формула:
Запишіть теорему Піфагора. Формула:, де
і
– катети прямокутного трикутника,
– гіпотенуза прямокутного трикутника.[3]
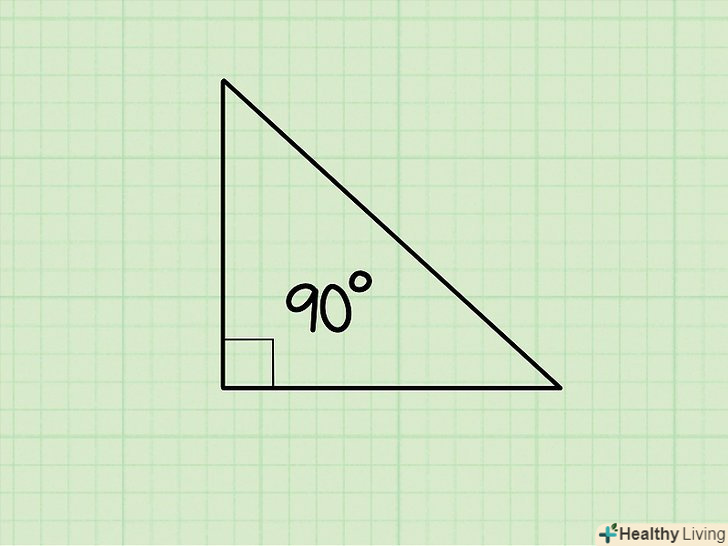
- Скористайтеся теоремою Піфагора, тому що кожна діагональ прямокутника ділить його на два рівних прямокутних трикутника.[4] причому сторони прямокутника-це катети трикутника, а діагональ прямокутника – гіпотенуза трикутника.
 У формулу підставте значення сторін. вони дані в задачі або їх потрібно виміряти. Значення сторін підставляються замість
У формулу підставте значення сторін. вони дані в задачі або їх потрібно виміряти. Значення сторін підставляються замістьі
.
- Наприклад, якщо довжина прямокутника дорівнює 4 см, а ширина – 3 см, формула запишеться так:
- Наприклад, якщо довжина прямокутника дорівнює 4 см, а ширина – 3 см, формула запишеться так:
 Довжину і ширину зведіть в квадрат, а потім складіть отримані результати.Пам'ятайте, що при зведенні числа в квадрат воно множиться на себе.
Довжину і ширину зведіть в квадрат, а потім складіть отримані результати.Пам'ятайте, що при зведенні числа в квадрат воно множиться на себе.- У нашому прикладі:
- У нашому прикладі:
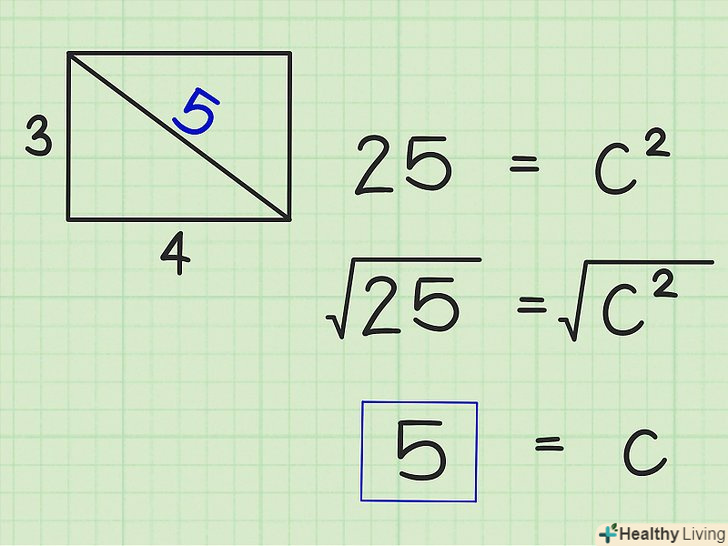
 Витягніть квадратний корінь з обох сторін рівняння.скористайтеся калькулятором, щоб швидко витягти квадратний корінь. Також можна скористатися онлайн-калькулятором.[5] Ви знайдете
Витягніть квадратний корінь з обох сторін рівняння.скористайтеся калькулятором, щоб швидко витягти квадратний корінь. Також можна скористатися онлайн-калькулятором.[5] Ви знайдете, тобто гіпотенузу трикутника, а значить і діагональ прямокутника.
- У нашому прикладі:
Таким чином, діагональ прямокутника з довжиною 4 см і шириною 3 см дорівнює 5 див.
- У нашому прикладі:
Метод2 З 3:
По площі і периметру
Метод2 З 3:
 Запишіть формулу для обчислення площі прямокутника. Формула:
Запишіть формулу для обчислення площі прямокутника. Формула:, де
– площа прямокутника,
– довжина прямокутника,
– ширина прямокутника.[6] (на малюнку замість S використано позначення А.)
 У формулу підставте значення площі прямокутника. це значення підставляється замість
У формулу підставте значення площі прямокутника. це значення підставляється замість.
- Наприклад, якщо площа прямокутника дорівнює 35 квадратних сантиметрів, формула запишеться так:
.
- Наприклад, якщо площа прямокутника дорівнює 35 квадратних сантиметрів, формула запишеться так:
 Перепишіть формулу так, щоб відокремити
Перепишіть формулу так, щоб відокремити. для цього розділіть обидві сторони рівняння на
. Потім отримане вираз потрібно підставити в формулу для обчислення периметра.
- У нашому прикладі:
.
- У нашому прикладі:
 Запишіть формулу для обчислення периметра прямокутника. Формула:
Запишіть формулу для обчислення периметра прямокутника. Формула:, де
– довжина прямокутника,
- ширина прямокутника.[7]
 У формулу підставте значення периметра прямокутника. це значення підставляється замість
У формулу підставте значення периметра прямокутника. це значення підставляється замість.
- Наприклад, якщо периметр прямокутника дорівнює 24 сантиметри, формула запишеться так:
.
- Наприклад, якщо периметр прямокутника дорівнює 24 сантиметри, формула запишеться так:
 Розділіть обидві сторони рівняння на 2. ви отримаєте суму сторін прямокутника, а саме
Розділіть обидві сторони рівняння на 2. ви отримаєте суму сторін прямокутника, а саме.
- У нашому прикладі:
.
- У нашому прикладі:
 У формулу підставте вираз для обчислення
У формулу підставте вираз для обчислення. цей вираз, отримане при відокремленні
.
- Наприклад, якщо при відокремленні
вийшла формула
, підставте її ліву сторону в формулу для обчислення периметра (замість w&#lt;/math&#gt;):
- Наприклад, якщо при відокремленні
 Позбудьтеся від дробу. для цього обидві частини рівняння помножте на
Позбудьтеся від дробу. для цього обидві частини рівняння помножте на.
- У нашому прикладі:
- У нашому прикладі:
 Прирівняйте рівняння до 0. для цього з обох сторін рівняння відніміть член зі змінною першого порядку.
Прирівняйте рівняння до 0. для цього з обох сторін рівняння відніміть член зі змінною першого порядку.- У нашому прикладі:
- У нашому прикладі:
 Упорядкуйте члени рівняння. першим членом буде член зі змінною другого порядку, потім член зі змінною першого порядку, а потім вільний член. При цьому не забудьте про знаки (»плюс «і» мінус"), які стоять перед членами. Зверніть увагу, що рівняння запишеться у вигляді квадратного рівняння.
Упорядкуйте члени рівняння. першим членом буде член зі змінною другого порядку, потім член зі змінною першого порядку, а потім вільний член. При цьому не забудьте про знаки (»плюс «і» мінус"), які стоять перед членами. Зверніть увагу, що рівняння запишеться у вигляді квадратного рівняння.- У нашому прикладі
запишеться так:
.
- У нашому прикладі
 Розкладіть квадратне рівняння на множники. щоб отримати докладні інструкції, прочитайте цю статтю.
Розкладіть квадратне рівняння на множники. щоб отримати докладні інструкції, прочитайте цю статтю.- У нашому прикладі рівняння
розкладається на множники так:
.
- У нашому прикладі рівняння
 Знайдіть
Знайдіть. для цього прирівняйте кожен множник до нуля і обчисліть
. Ви отримаєте два значення (це коріння рівняння), які в разі прямокутника є його довжиною і шириною.
- У нашому прикладі:
.
таким чином, довжина і ширина прямокутника рівні 7 см і 5 см, відповідно.
- У нашому прикладі:
 Запишіть теорему Піфагора. Формула:
Запишіть теорему Піфагора. Формула:, де
і
– катети прямокутного трикутника,
– гіпотенуза прямокутного трикутника.[8]
- Скористайтеся теоремою Піфагора, тому що кожна діагональ прямокутника ділить його на два рівних прямокутних трикутника.[9] причому сторони прямокутника-це катети трикутника, а діагональ прямокутника – гіпотенуза трикутника.
 У формулу підставте значення довжини і ширини. ці значення підставляються замість
У формулу підставте значення довжини і ширини. ці значення підставляються замістьі
(в довільному порядку).
- Наприклад, якщо довжина і ширина прямокутника рівні 7 см і 5 см, формула запишеться так:
.
- Наприклад, якщо довжина і ширина прямокутника рівні 7 см і 5 см, формула запишеться так:
 Довжину і ширину зведіть в квадрат, а потім складіть отримані результати.Пам'ятайте, що при зведенні числа в квадрат воно множиться на себе.
Довжину і ширину зведіть в квадрат, а потім складіть отримані результати.Пам'ятайте, що при зведенні числа в квадрат воно множиться на себе.- У нашому прикладі:
- У нашому прикладі: