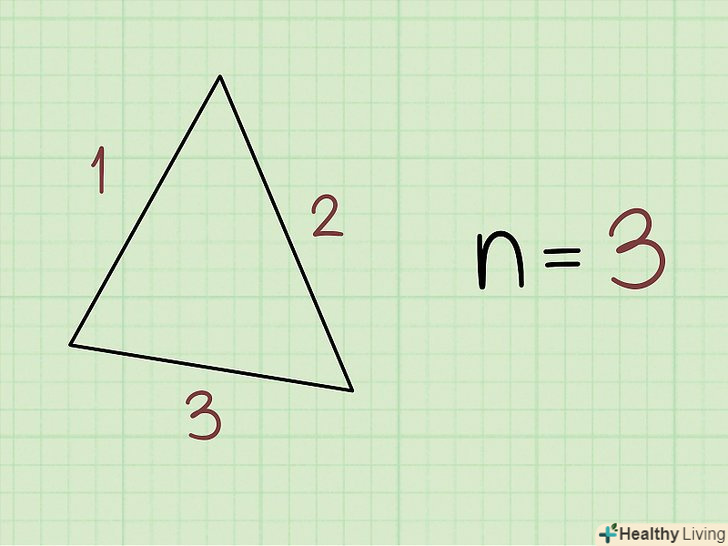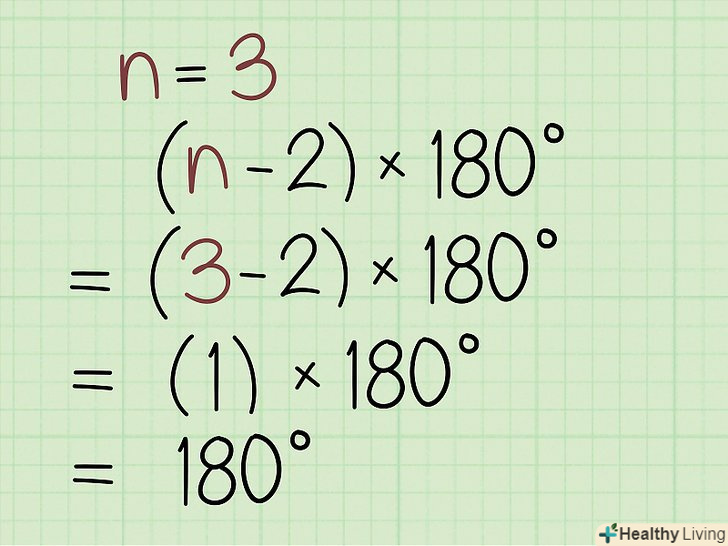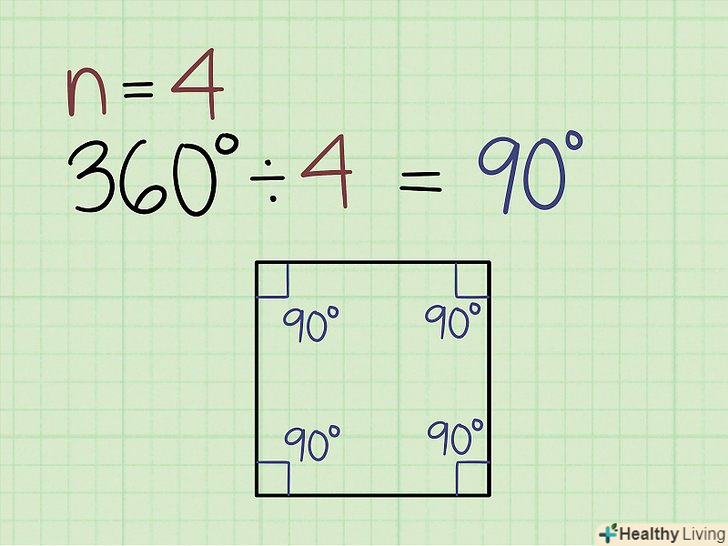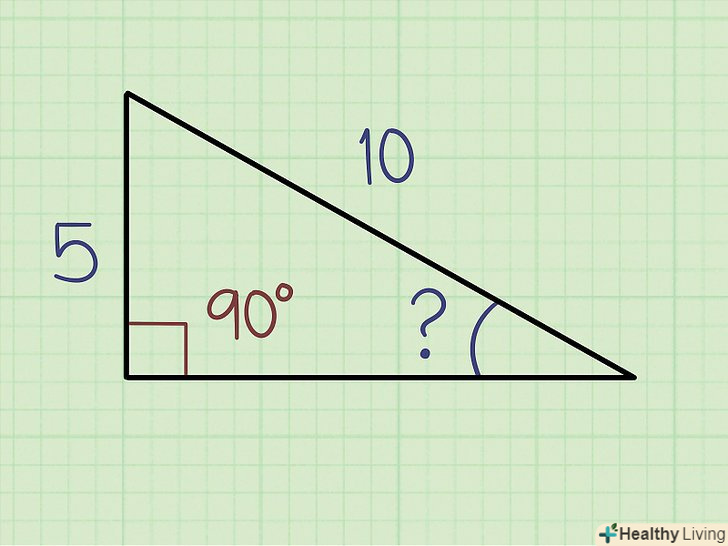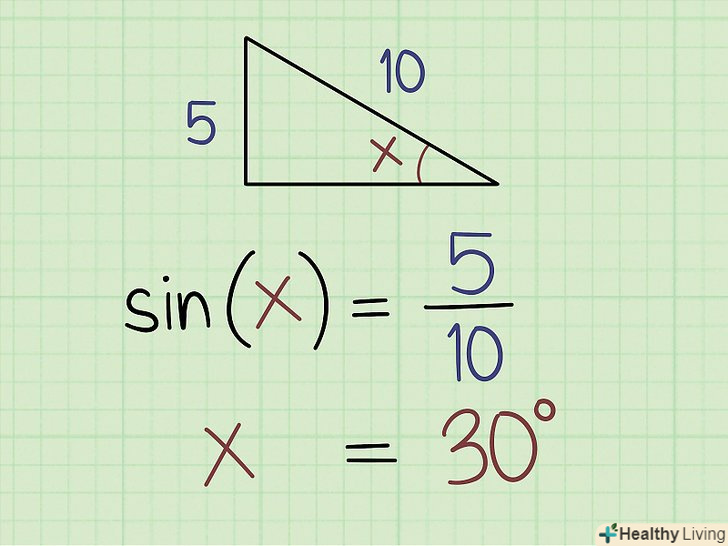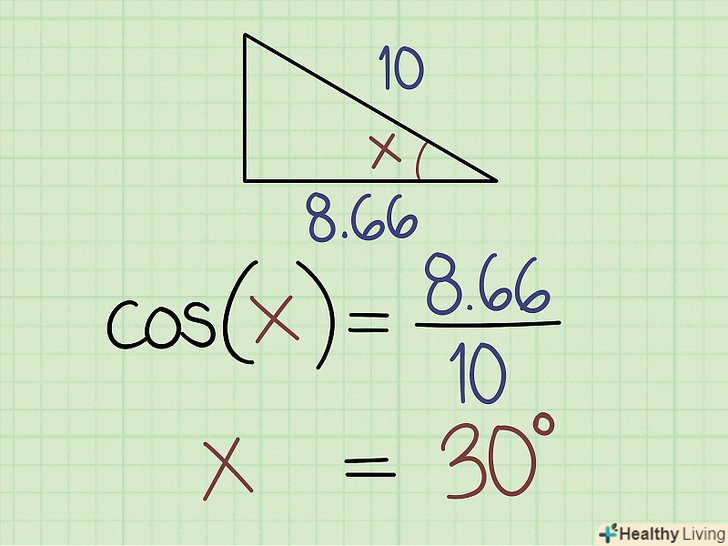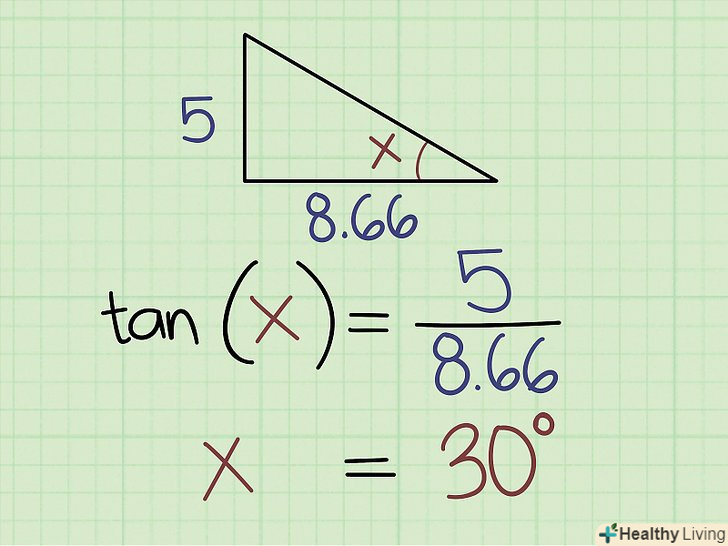В геометрії кут-це фігура, яка утворена двома променями, які виходять з однієї точки (вона називається вершиною кута). У більшості випадків одиницею вимірювання кута є градус ( ° ) - пам'ятайте, що повний кут або один оборот дорівнює 360°. Знайти значення кута багатокутника можна за його типом і значенням інших кутів, а якщо дано прямокутний трикутник, кут можна обчислити по двох сторонах. Більш того, кут можна виміряти за допомогою транспортира або обчислити за допомогою графічного калькулятора.
Кроки
Метод1 З 2:
Як знайти внутрішні кути багатокутника
 Порахуйте число сторін багатокутника.щоб обчислити внутрішні кути багатокутника, спочатку потрібно визначити, скільки у багатокутника сторін. Зверніть увагу, що число сторін багатокутника дорівнює числу його кутів.[1]
Порахуйте число сторін багатокутника.щоб обчислити внутрішні кути багатокутника, спочатку потрібно визначити, скільки у багатокутника сторін. Зверніть увагу, що число сторін багатокутника дорівнює числу його кутів.[1]- Наприклад, у трикутника 3 сторони і 3 внутрішніх кутів, а у квадрата 4 сторони і 4 внутрішніх кутів.
 Обчисліть суму всіх внутрішніх кутів багатокутника.для цього скористайтеся наступною формулою: (n - 2) x 180. У цій формулі n-це кількість сторін багатокутника. Далі наведені суми кутів часто зустрічаються багатокутників:[2]
Обчисліть суму всіх внутрішніх кутів багатокутника.для цього скористайтеся наступною формулою: (n - 2) x 180. У цій формулі n-це кількість сторін багатокутника. Далі наведені суми кутів часто зустрічаються багатокутників:[2]- Сума кутів трикутника (багатокутника з 3-ма сторонами) дорівнює 180°.
- Сума кутів чотирикутника (багатокутника з 4-ма сторонами) дорівнює 360°.
- Сума кутів п'ятикутника (багатокутника з 5-ма сторонами) дорівнює 540°.
- Сума кутів шестикутника (багатокутника з 6-ма сторонами) дорівнює 720°.
- Сума кутів восьмикутника (багатокутника з 8-ма сторонами) дорівнює 1080°.
 Розділіть суму всіх кутів правильного багатокутника на число кутів. правильний багатокутник це багатокутник з рівними сторонами і рівними кутами. Наприклад, кожен кут рівностороннього трикутника обчислюється так: 180 ÷ 3 = 60°, а кожен кут квадрата знаходиться так: 360 ÷ 4 = 90°.[3]
Розділіть суму всіх кутів правильного багатокутника на число кутів. правильний багатокутник це багатокутник з рівними сторонами і рівними кутами. Наприклад, кожен кут рівностороннього трикутника обчислюється так: 180 ÷ 3 = 60°, а кожен кут квадрата знаходиться так: 360 ÷ 4 = 90°.[3]- Рівносторонній трикутник і квадрат-це правильні багатокутники. А біля будівлі Пентагону (Вашингтон, США) і дорожнього знака «Стоп» форма правильного восьмикутника.
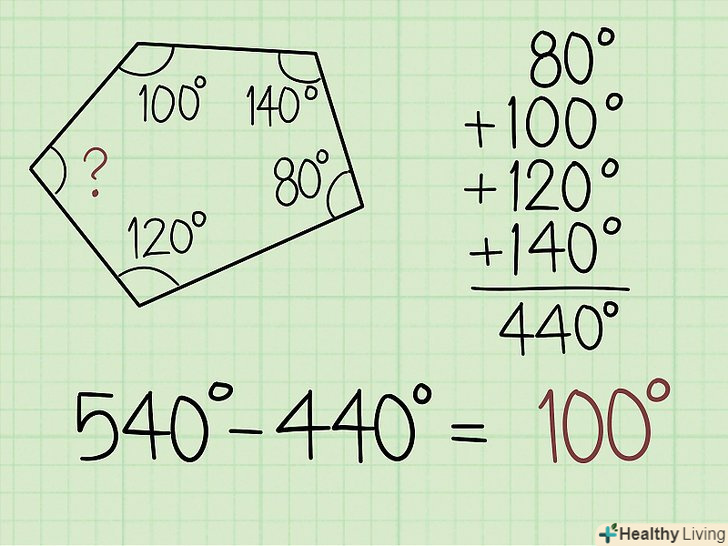
 Відніміть суму всіх відомих кутів із загальної суми кутів неправильного багатокутника. якщо сторони багатокутника не рівні один одному, і його кути також не рівні один одному, спочатку складіть відомі кути багатокутника. Тепер отримане значення відніміть з суми всіх кутів багатокутника - так ви знайдете невідомий кут.[4]
Відніміть суму всіх відомих кутів із загальної суми кутів неправильного багатокутника. якщо сторони багатокутника не рівні один одному, і його кути також не рівні один одному, спочатку складіть відомі кути багатокутника. Тепер отримане значення відніміть з суми всіх кутів багатокутника - так ви знайдете невідомий кут.[4]- Наприклад, якщо дано, що 4 кути п'ятикутника рівні 80°, 100°, 120° і 140°, складіть ці числа: 80 + 100 + 120 + 140 = 440. Тепер відніміть це значення з суми всіх кутів п'ятикутника; ця сума дорівнює 540°: 540 - 440 = 100°. Таким чином, невідомий кут дорівнює 100°.
Порада: невідомий кут деяких багатокутників можна обчислити, якщо знати властивості фігури. Наприклад, в рівнобедреному трикутнику дві сторони рівні і два кути рівні; в паралелограмі (це чотирикутник) протилежні сторони рівні і протилежні кути рівні.
Метод2 З 2:
Як знайти кути прямокутного трикутника
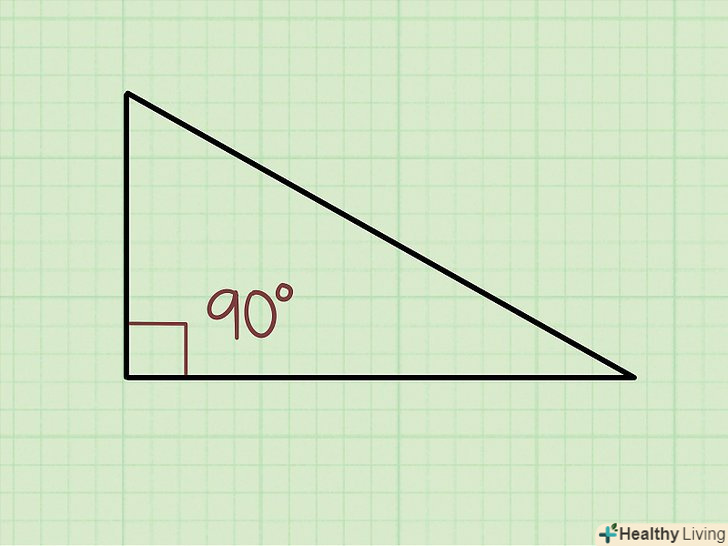
 Пам'ятайте, що в будь-якому прямокутному трикутнику один кут завжди дорівнює 90°. це так, навіть якщо прямий кут ніяк не відзначений або його значення не вказано. Таким чином, один кут прямокутного трикутника завжди відомий, а інші кути можна обчислити за допомогою тригонометрії.[5]
Пам'ятайте, що в будь-якому прямокутному трикутнику один кут завжди дорівнює 90°. це так, навіть якщо прямий кут ніяк не відзначений або його значення не вказано. Таким чином, один кут прямокутного трикутника завжди відомий, а інші кути можна обчислити за допомогою тригонометрії.[5] Виміряйте довжину двох сторін трикутника.найдовша сторона прямокутного трикутника називається гіпотенузою. Прилегла сторона це сторона, яка знаходиться біля невідомого кута. Протилежна сторона-це сторона, яка знаходиться навпроти невідомого кута. Виміряйте дві сторони, щоб обчислити невідомі кути трикутника.[6]
Виміряйте довжину двох сторін трикутника.найдовша сторона прямокутного трикутника називається гіпотенузою. Прилегла сторона це сторона, яка знаходиться біля невідомого кута. Протилежна сторона-це сторона, яка знаходиться навпроти невідомого кута. Виміряйте дві сторони, щоб обчислити невідомі кути трикутника.[6]Порада: скористайтеся графічним калькулятором, щоб вирішити рівняння, або знайдіть онлайн-таблицю зі значеннями синусів, косинусів і тангенсів.
 Обчисліть синус кута, якщо вам відомі протилежна сторона і гіпотенуза.для цього підставте значення в рівняння: sin(x) = протилежна сторона ÷ гіпотенуза. Наприклад, протилежна сторона дорівнює 5 см, а гіпотенуза дорівнює 10 см.розділіть 5/10 = 0,5. Таким чином, sin (x) = 0,5, тобто x = sin-1 (0,5).[7]
Обчисліть синус кута, якщо вам відомі протилежна сторона і гіпотенуза.для цього підставте значення в рівняння: sin(x) = протилежна сторона ÷ гіпотенуза. Наприклад, протилежна сторона дорівнює 5 см, а гіпотенуза дорівнює 10 см.розділіть 5/10 = 0,5. Таким чином, sin (x) = 0,5, тобто x = sin-1 (0,5).[7]- Якщо у вас є графічний калькулятор, введіть 0,5 і натисніть клавішу sin-1. Якщо у вас немає такого калькулятора, використовуйте онлайн-таблицю, щоб знайти значення кута. У нашому прикладі кут дорівнює 30°.
 Обчисліть косинус кута, якщо вам відомі прилегла сторона і гіпотенуза.для цього підставте значення в рівняння: cos (x) = прилегла сторона ÷ гіпотенуза. Наприклад, прилегла сторона дорівнює 1,67 см, а гіпотенуза дорівнює 2 см.розділіть 1,67/2 = 0,83. Таким чином, cos (x) = 0,83, тобто x = cos-1 (0,83).[8]
Обчисліть косинус кута, якщо вам відомі прилегла сторона і гіпотенуза.для цього підставте значення в рівняння: cos (x) = прилегла сторона ÷ гіпотенуза. Наприклад, прилегла сторона дорівнює 1,67 см, а гіпотенуза дорівнює 2 см.розділіть 1,67/2 = 0,83. Таким чином, cos (x) = 0,83, тобто x = cos-1 (0,83).[8]- Якщо у вас є графічний калькулятор, введіть 0,83 і натисніть клавішу cos-1. Якщо у вас немає такого калькулятора, використовуйте онлайн-таблицю, щоб знайти значення кута. У нашому прикладі кут дорівнює 33,6°.
 Обчисліть тангенс кута, якщо вам відомі протилежна і прилегла сторони.для цього підставте значення в рівняння: tg(x) = протилежна сторона ÷ прилегла сторона. Наприклад, протилежна сторона дорівнює 75 см, а прилегла сторона дорівнює 75 см.розділіть 75/100 = 0,75. Таким чином, tg (x) = 0,75, тобто x = tg-1 (0,75).[9]
Обчисліть тангенс кута, якщо вам відомі протилежна і прилегла сторони.для цього підставте значення в рівняння: tg(x) = протилежна сторона ÷ прилегла сторона. Наприклад, протилежна сторона дорівнює 75 см, а прилегла сторона дорівнює 75 см.розділіть 75/100 = 0,75. Таким чином, tg (x) = 0,75, тобто x = tg-1 (0,75).[9]- Якщо у вас є графічний калькулятор, введіть 0,75 і натисніть клавішу TG-1. Якщо у вас немає такого калькулятора, використовуйте онлайн-таблицю, щоб знайти значення кута. У нашому прикладі кут дорівнює 36,9°.
Поради
- Назви кутів відповідають їх значенням. Кут в 90° - це прямий кут. Кут в 180° - це розгорнутий кут. Кут, який лежить між 0 ° і 90° - це гострий кут. Кут, який лежить між 90° і 180° - це тупий кут. Кут, який лежить між 180° і 360° - це невипуклий кут.
- Якщо сума двох кутів дорівнює 90°, вони називаються додатковими. Запам'ятайте: два гострих кута прямокутного трикутника завжди є додатковими. Якщо ж сума двох кутів дорівнює 180°, вони називаються суміжними.
Джерела
- ↑ Https://www.mathsisfun.com/geometry/interior-angles-polygons.html
- ↑ Https://www.mathsisfun.com/geometry/interior-angles-polygons.html
- ↑ Https://www.bbc.co.uk/bitesize/guides/zshb97h/revision/6
- ↑ Https://www.mathopenref.com/polygoninteriorangles.html
- ↑ Https://www.mathsisfun.com/algebra/trig-finding-angle-right-triangle.html
- ↑ Https://www.mathsisfun.com/algebra/trig-finding-angle-right-triangle.html
- ↑ Https://sciencing.com/angle-right-triangle-8159743.html
- ↑ Https://sciencing.com/angle-right-triangle-8159743.html
- ↑ Https://sciencing.com/angle-right-triangle-8159743.html