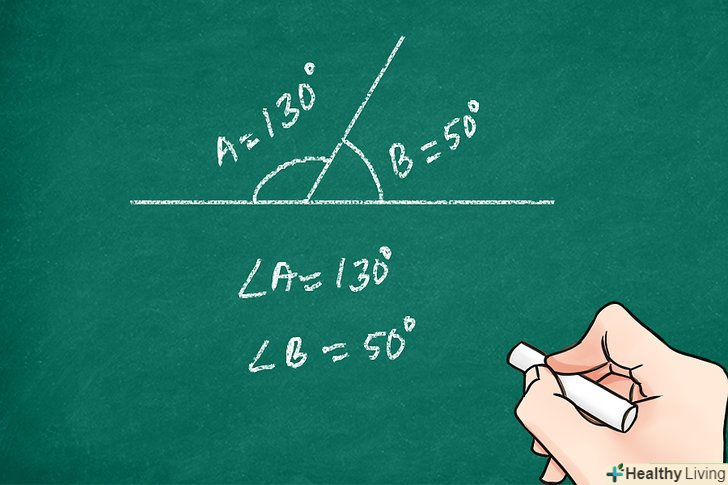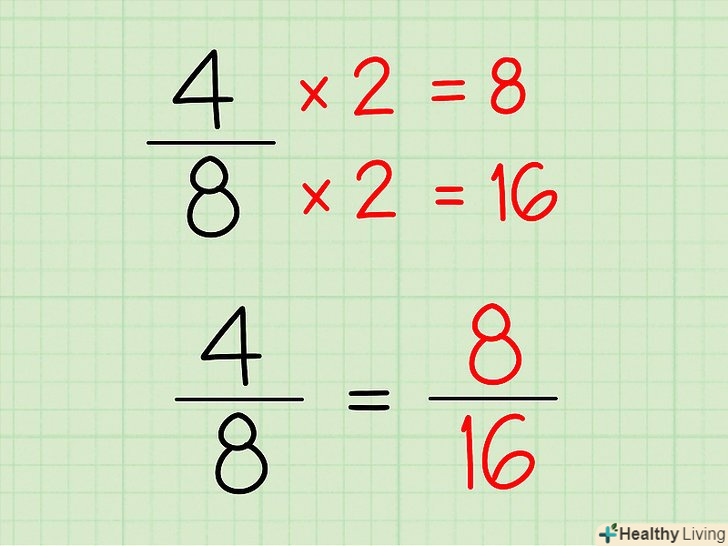Знаходження математичного доказу може виявитися непростим завданням, але вам допоможе знання математики і вміння оформити доказ. На жаль, не існує швидких і простих методів навчитися вирішувати математичні завдання. Необхідно як слід вивчити предмет і запам'ятати основні теореми і визначення, які стануть в нагоді вам при доказі того чи іншого математичного постулату. Вивчайте приклади математичних доказів і тренуйтеся самі-це допоможе вам удосконалити свою майстерність.
Кроки
Метод1З 3:
Зрозумійте умову задачі
Метод1З 3:
 Визначте, що потрібно знайти.насамперед необхідно з'ясувати, що саме слід довести. Крім іншого, цим буде визначатися останнє твердження У вашому доказі. На даному етапі слід також зробити певні допущення, в рамках яких ви будете працювати. Щоб краще зрозуміти завдання і приступити до її вирішення, з'ясуйте, що потрібно довести, і зробіть необхідні припущення.
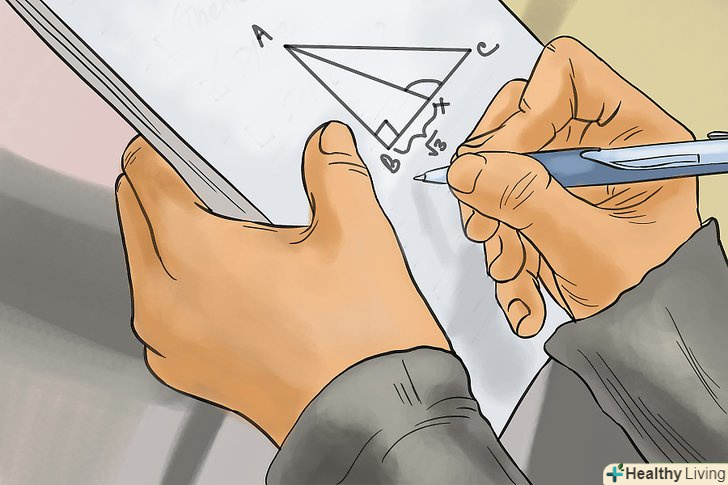
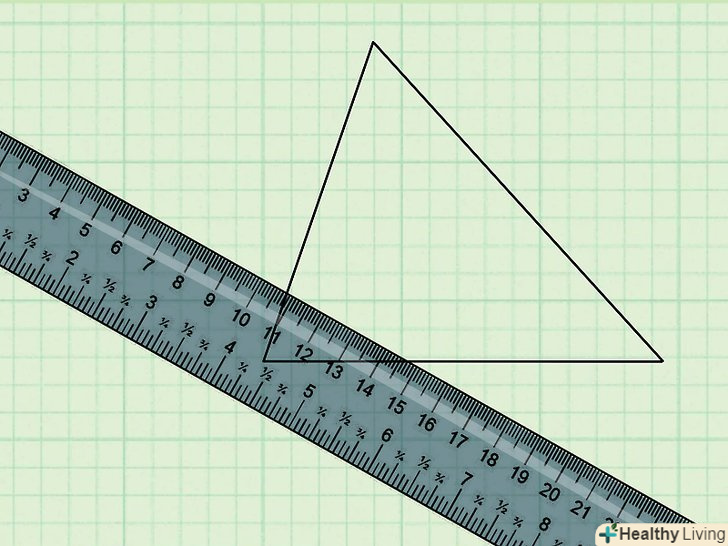
Визначте, що потрібно знайти.насамперед необхідно з'ясувати, що саме слід довести. Крім іншого, цим буде визначатися останнє твердження У вашому доказі. На даному етапі слід також зробити певні допущення, в рамках яких ви будете працювати. Щоб краще зрозуміти завдання і приступити до її вирішення, з'ясуйте, що потрібно довести, і зробіть необхідні припущення. Зробіть малюнок.при вирішенні математичних задач іноді корисно зобразити їх у вигляді малюнка або схеми. Це особливо важливо в разі геометричних завдань-малюнок допомагає наочно представити умову і значно полегшує пошук рішення.
Зробіть малюнок.при вирішенні математичних задач іноді корисно зобразити їх у вигляді малюнка або схеми. Це особливо важливо в разі геометричних завдань-малюнок допомагає наочно представити умову і значно полегшує пошук рішення.- При створенні малюнка або схеми використовуйте наведені в умові дані. Відзначте на малюнку відомі і невідомі величини.
- Малюнок полегшить вам пошук докази.
 Вивчіть докази схожих теорем.якщо вам не вдається відразу знайти рішення, знайдіть подібні теореми і подивіться, як вони доводяться.
Вивчіть докази схожих теорем.якщо вам не вдається відразу знайти рішення, знайдіть подібні теореми і подивіться, як вони доводяться.- Врахуйте, що необхідно аргументувати кожен крок докази. Подивіться, як доводяться різні теореми в інтернеті або підручниках з математики.[1]
 Задавайте питання.нічого страшного, якщо вам не вдасться відразу ж знайти доказ. Якщо вам щось неясно, запитайте про це вчителя або однокласників. Можливо, у ваших товаришів виникли ті ж питання, і ви зможете розібратися з ними разом. Краще задати кілька питань, ніж знову і знову безуспішно намагатися знайти доказ.
Задавайте питання.нічого страшного, якщо вам не вдасться відразу ж знайти доказ. Якщо вам щось неясно, запитайте про це вчителя або однокласників. Можливо, у ваших товаришів виникли ті ж питання, і ви зможете розібратися з ними разом. Краще задати кілька питань, ніж знову і знову безуспішно намагатися знайти доказ.- Підійдіть до вчителя після уроків і з'ясуйте всі неясні питання.
Метод2 З 3:
Сформулюйте доказ
Метод2 З 3:
 Сформулюйте математичний доказ.математичним доказом називають підкріплену теоремами і визначеннями послідовність тверджень, яка доводить будь-якої математичний постулат.[2] докази є єдиним способом визначити, що те чи інше твердження вірно в математичному сенсі.
Сформулюйте математичний доказ.математичним доказом називають підкріплену теоремами і визначеннями послідовність тверджень, яка доводить будь-якої математичний постулат.[2] докази є єдиним способом визначити, що те чи інше твердження вірно в математичному сенсі.- Вміння записати математичний доказ свідчить про глибоке розуміння задачі і володіння необхідними інструментами (леммами, теоремами і визначеннями).
- Суворі докази допоможуть вам по-новому поглянути на математику і відчути її притягальну силу. Просто спробуйте довести будь-яке твердження, щоб отримати уявлення про математичні методи.
 Врахуйте свою аудиторію.перш ніж приступити до запису докази, слід подумати про те, Для кого воно призначене, і врахувати рівень знань цих людей. Якщо ви записуєте доказ для подальшої публікації в науковому журналі, воно буде відрізнятися від того випадку, коли ви виконуєте шкільне завдання.[3]
Врахуйте свою аудиторію.перш ніж приступити до запису докази, слід подумати про те, Для кого воно призначене, і врахувати рівень знань цих людей. Якщо ви записуєте доказ для подальшої публікації в науковому журналі, воно буде відрізнятися від того випадку, коли ви виконуєте шкільне завдання.[3]- Знання цільової аудиторії дозволить вам записати доказ з урахуванням підготовки читачів, щоб вони зрозуміли його.
 Визначте тип доказу.є кілька видів математичних доказів, і вибір конкретної форми залежить від цільової аудиторії і розв'язуваної задачі. Якщо ви не знаєте, який вид вибрати, порадьтеся зі своїм учителем. У старших класах школи потрібно оформляти докази в дві колонки.[4]
Визначте тип доказу.є кілька видів математичних доказів, і вибір конкретної форми залежить від цільової аудиторії і розв'язуваної задачі. Якщо ви не знаєте, який вид вибрати, порадьтеся зі своїм учителем. У старших класах школи потрібно оформляти докази в дві колонки.[4]- При запису докази в дві колонки в одну заносять вихідні дані і твердження, а в другу — відповідні докази цих тверджень. Таку форму запису часто використовують при вирішенні геометричних задач.
- При менш формальному записі доказів використовують граматично правильні конструкції і меншу кількість символів. На більш високих рівнях слід застосовувати саме цей запис.
 Зробіть начерк докази у вигляді двох колонок.така форма допомагає впорядкувати думки і послідовно вирішити задачу. Розділіть сторінку навпіл вертикальною лінією і запишіть вихідні дані і витікаючі з них твердження в лівій частині. Праворуч навпроти кожного твердження запишіть відповідні визначення та теореми.
Зробіть начерк докази у вигляді двох колонок.така форма допомагає впорядкувати думки і послідовно вирішити задачу. Розділіть сторінку навпіл вертикальною лінією і запишіть вихідні дані і витікаючі з них твердження в лівій частині. Праворуч навпроти кожного твердження запишіть відповідні визначення та теореми.- Наприклад:[5]
- Кути A і B є суміжними-дано;
- Кут ABC є розгорнутим-визначення розгорнутого кута;
- Величина кута ABC становить 180° - визначення прямої лінії;
- Кут a + кут B = кут ABC-правило складання кутів;
- Кут a + кут B = 180° — підстановка;
- Кут A є додатковим до кута B-визначення додаткових кутів;
- Що і потрібно довести.
 Запишіть доказ з двох колонок у вигляді неформального доказу.візьміть за основу запис у вигляді двох колонок і запишіть доказ в більш короткій формі з меншою кількістю символів і скорочень.
Запишіть доказ з двох колонок у вигляді неформального доказу.візьміть за основу запис у вигляді двох колонок і запишіть доказ в більш короткій формі з меншою кількістю символів і скорочень.- Наприклад: припустимо, що кути а і В є суміжними. Згідно з гіпотезою, ці кути доповнюють один одного. Будучи суміжними, кут A і кут B утворюють пряму лінію. Якщо сторони кута утворюють пряму лінію, такий кут дорівнює 180°. Складемо кути A і B і отримаємо пряму лінію ABC. Таким чином, сума кутів A і B дорівнює 180°, тобто ці кути є додатковими. Що і було потрібно довести.
Метод3 З 3:
Запишіть доказ
Метод3 З 3:
 Освойте мову доказів.для запису математичних доказів використовують стандартні твердження і фрази. Необхідно вивчити ці фрази і знати, як ними користуватися.[6]
Освойте мову доказів.для запису математичних доказів використовують стандартні твердження і фрази. Необхідно вивчити ці фрази і знати, як ними користуватися.[6]- Фраза "Якщо a, ТО B" означає, що якщо твердження а вірно, то має бути вірним і твердження в.[7]
- " a тоді і тільки тоді, якщо B " означає, що твердження A і B або вірні, або невірні одночасно. Така конструкція еквівалентна двом одночасним твердженням:" якщо A, то B "і"якщо A не виконується, то не виконується і B".
- "a тільки якщо B "еквівалентно" якщо в, то А", тому така конструкція зустрічається нечасто. Проте необхідно пам'ятати про неї.
- При записі доказів намагайтеся замість особистого займенника "я" використовувати "ми".[8]
 Запишіть всі вихідні дані. при складанні докази насамперед слід визначити і виписати все, що дано в задачі. В цьому випадку ви будете мати перед очима всі вихідні дані, на підставі яких необхідно отримати рішення. Уважно прочитайте умову завдання і випишіть все, що в ньому дано.
Запишіть всі вихідні дані. при складанні докази насамперед слід визначити і виписати все, що дано в задачі. В цьому випадку ви будете мати перед очима всі вихідні дані, на підставі яких необхідно отримати рішення. Уважно прочитайте умову завдання і випишіть все, що в ньому дано.- Наприклад: доведіть, що два суміжних кута (кут A і кут B) доповнюють один одного.[9]
- Дано: суміжні кути A і B.
- Довести: кут A є додатковим до кута B.
 Визначте всі змінні.крім запису вихідних даних корисно також виписати інші змінні. Щоб читачам було зручніше, запишіть змінні на самому початку. Якщо змінні не визначені, читач може заплутатися і не зрозуміти ваше доказ.
Визначте всі змінні.крім запису вихідних даних корисно також виписати інші змінні. Щоб читачам було зручніше, запишіть змінні на самому початку. Якщо змінні не визначені, читач може заплутатися і не зрозуміти ваше доказ.- Не використовуйте в ході доказу невизначені раніше змінні.
- Наприклад: у розглянутій вище задачі змінними є величини кутів A і B.
 Спробуйте знайти доказ у зворотному порядку.багато завдань легше вирішувати в зворотній послідовності. Почніть з того, що потрібно довести, і подумайте, як можна пов'язати висновки з вихідною умовою.[10]
Спробуйте знайти доказ у зворотному порядку.багато завдань легше вирішувати в зворотній послідовності. Почніть з того, що потрібно довести, і подумайте, як можна пов'язати висновки з вихідною умовою.[10]- Перечитайте початкові і кінцеві кроки і подивіться, чи не схожі вони один на одного. Використовуйте при цьому початкові умови, визначення та схожі докази з інших завдань.
- Задавайте самому собі питання і просувайтеся вперед. Щоб довести окремі твердження, запитуйте себе: "Чому це саме так?"- і: "чи може це виявитися неправильним?”
- Не забувайте послідовно записувати окремі кроки, поки не отримаєте кінцевий результат.
- Наприклад: якщо кути A і B є додатковими, їх сума повинна становити 180°. Згідно з визначенням суміжних кутів, кути A і B утворюють пряму лінію ABC. Так як лінія утворює кут 180°, в сумі кути A і B дають 180°.
 Розташуйте окремі кроки докази так, щоб воно було послідовним і логічним.почніть з самого початку і просувайтеся до доказуваної тези. Хоча іноді і корисно почати пошук докази з кінця, при його записи необхідно дотримуватися правильного порядку.[11] окремі тези повинні слідувати один за іншим, щоб доказ було логічним і не викликало сумнівів.
Розташуйте окремі кроки докази так, щоб воно було послідовним і логічним.почніть з самого початку і просувайтеся до доказуваної тези. Хоча іноді і корисно почати пошук докази з кінця, при його записи необхідно дотримуватися правильного порядку.[11] окремі тези повинні слідувати один за іншим, щоб доказ було логічним і не викликало сумнівів.- Для початку розгляньте висунуті припущення.
- Підтвердіть зроблені твердження простими і очевидними кроками, щоб у читача не виникало сумнівів в їх правильності.
- Іноді доводиться не один раз переписувати доказ. Продовжуйте групувати твердження та їх докази до тих пір, поки не досягнете найбільш логічного побудови.
- Наприклад: почнемо з початку.
- Кути A і B є суміжними.
- Сторони кута ABC утворюють пряму лінію.
- Кут ABC становить 180°.
- Кут a + кут B = кут ABC.
- Кут a + кут B = кут 180°.
- Кут A є додатковим до кута B.
 Не використовуйте в доказі стрілочки і скорочення.при роботі з чорновим варіантом можна користуватися різними скороченнями і символами, проте не включайте їх в остаточний чистовий варіант, так як це може заплутати читачів. Використовуйте замість цього такі слова, як" отже "і"тоді".[12]
Не використовуйте в доказі стрілочки і скорочення.при роботі з чорновим варіантом можна користуватися різними скороченнями і символами, проте не включайте їх в остаточний чистовий варіант, так як це може заплутати читачів. Використовуйте замість цього такі слова, як" отже "і"тоді".[12]- Як винятки допускаються зрозумілі скорочення, наприклад "тобто" (тобто), однак використовуйте їх належним чином.[13]
 Підтверджуйте кожну тезу теоремою, законом або визначенням. доказ повинен бути бездоганним. Не можна робити нічим не підкріплених тверджень. Подивіться, як будуються докази завдань, схожих з вашою.
Підтверджуйте кожну тезу теоремою, законом або визначенням. доказ повинен бути бездоганним. Не можна робити нічим не підкріплених тверджень. Подивіться, як будуються докази завдань, схожих з вашою.- Спробуйте застосувати знайдене доказ до випадків, коли воно не повинно виконуватися, і подивіться, чи так це. Якщо доказ підходить і для таких випадків, перевірте, де ви допустили помилку.
- Часто докази геометричних задач записуються у вигляді двох колонок. Справа пишуться твердження, а зліва наводяться їх докази. Водночас у публікаціях математичні докази оформляються у вигляді абзаців з відповідною граматикою.
 Завершуйте докази фразою"що і потрібно довести".в кінці доказу повинен стояти доказувана теза. Після нього слід написати " що і було потрібно довести "(скорочено" ч.т. д. " або символ у вигляді зафарбованого квадрата) — це означає, що доказ завершено.[14]
Завершуйте докази фразою"що і потрібно довести".в кінці доказу повинен стояти доказувана теза. Після нього слід написати " що і було потрібно довести "(скорочено" ч.т. д. " або символ у вигляді зафарбованого квадрата) — це означає, що доказ завершено.[14]- На латині фразі" що і було потрібно довести "відповідає абревіатура Q. E. D. (quod erat demonstrandum, тобто"що і потрібно показати").
- Якщо ви сумніваєтеся в правильності доказу, просто напишіть кілька фраз про те, до якого висновку ви прийшли і чому він важливий.
Поради
- Вся наведена в доказі інформація повинна служити досягненню поставленої мети. Не включайте в доказ те, без чого можна обійтися.
Джерела
- ↑ Http://www.proofwiki.org/wiki/Main_Page
- ↑ Http://www.math.uconn.edu/~hurley/math315/proofgoldberger.pdf
- ↑ Https://www.math.washington.edu/~lee/Writing/writing-proofs.pdf
- ↑ Http://www.homeschoolmath.net/teaching/two-column-proof.php
- ↑ Http://www.ohschools.k12.oh.us/userfiles/225/Classes/72/6per2-6day2oct10.pdf
- ↑ Https://math.berkeley.edu/~hutching/teach/proofs.pdf
- ↑ Http://www.math.ucsd.edu/~ebender/proofs.html
- ↑ Http://www.ms.uky.edu/~kott/proof_help.pdf
- ↑ Http://www.ohschools.k12.oh.us/userfiles/225/Classes/72/6per2-6day2oct10.pdf