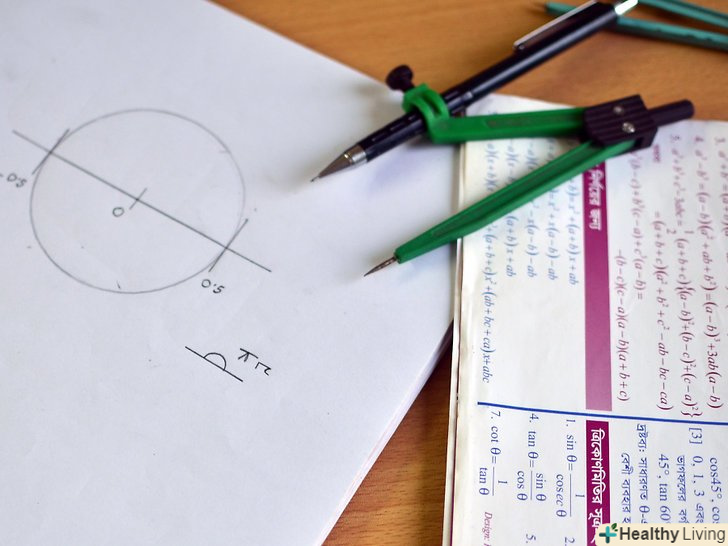Одинична окружність є чудовим інструментом при тригонометричних операціях; якщо ви дійсно зрозумієте дії з одиничною окружністю, тригонометрія дасться вам набагато легше.
Кроки
 Що таке одинична окружність.одинична окружність - це коло з радіусом, рівним 1, і з центром на початку координат. Згадайте, що рівняння кола виглядає як x2+y2=1. Така окружність може бути використана для знаходження деяких "особливих" тригонометричних співвідношень, а також при побудові графічних зображень. За допомогою неї і укладеної в ній лінії можна оцінювати і чисельні значення тригонометричних функцій.
Що таке одинична окружність.одинична окружність - це коло з радіусом, рівним 1, і з центром на початку координат. Згадайте, що рівняння кола виглядає як x2+y2=1. Така окружність може бути використана для знаходження деяких "особливих" тригонометричних співвідношень, а також при побудові графічних зображень. За допомогою неї і укладеної в ній лінії можна оцінювати і чисельні значення тригонометричних функцій. Запам'ятайте 6 тригонометричних співвідношень. Пам'ятайте, що
Запам'ятайте 6 тригонометричних співвідношень. Пам'ятайте, що- Sinθ=протилежний катет / гіпотенуза
- Cosθ=прилеглий катет / гіпотенуза
- Tgθ=протилежний катет / прилеглий катет
- Cosecθ=1/sin
- Secθ=1/cos
- Ctgθ=1/tg.
 Що таке радіан.радіан-один із заходів для визначення величини кута. Один радіан - це величина кута між двома радіусами, проведеними так, що довжина дуги між ними дорівнює величині радіуса. Зауважте, що при цьому величина і розташування кола не грають ніякої ролі. Слід також знати, чому дорівнює число радіан для повного кола (360 градусів). Згадайте, що довжина кола дорівнює 2πR, що перевищує довжину радіуса в 2π рази. Оскільки за визначенням 1 радіан - це кут між кінцями дуги, довжина якої дорівнює радіусу, в повній окружності укладений кут, рівний 2π радіан.
Що таке радіан.радіан-один із заходів для визначення величини кута. Один радіан - це величина кута між двома радіусами, проведеними так, що довжина дуги між ними дорівнює величині радіуса. Зауважте, що при цьому величина і розташування кола не грають ніякої ролі. Слід також знати, чому дорівнює число радіан для повного кола (360 градусів). Згадайте, що довжина кола дорівнює 2πR, що перевищує довжину радіуса в 2π рази. Оскільки за визначенням 1 радіан - це кут між кінцями дуги, довжина якої дорівнює радіусу, в повній окружності укладений кут, рівний 2π радіан. Вмійте перевести радіани в градуси.у повній окружності міститься 2π радіан, або 360 градусів. Таким чином:
Вмійте перевести радіани в градуси.у повній окружності міститься 2π радіан, або 360 градусів. Таким чином:- 2π радіан=360 градусів
- 1 радіан=(360/2π) градусів
- 1 радіан=(180 / π) градусів
- І
- 360 градусів=2π радіан
- 1 градус=(2π / 360) радіан
- 1 градус=(π/180) радіан
 Вивчіть "особливі" кути.ці кути в радіанах складають π/6, π/3, π/4, π / 2, π і добутки даних величин (наприклад, 5π/6)
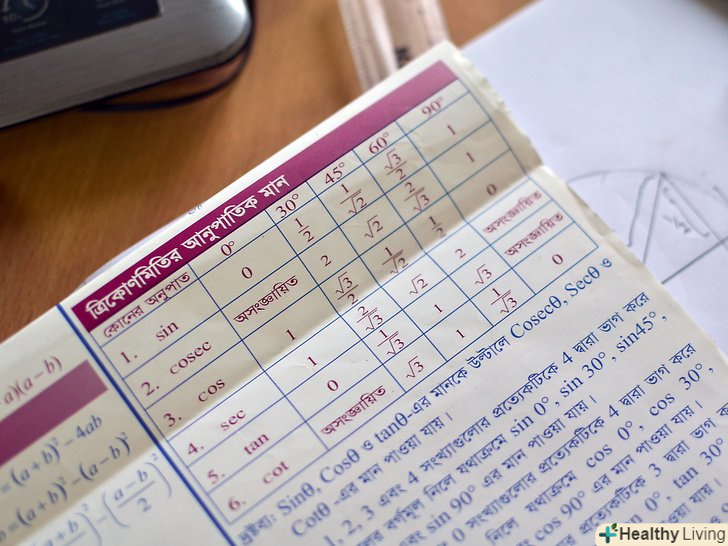
Вивчіть "особливі" кути.ці кути в радіанах складають π/6, π/3, π/4, π / 2, π і добутки даних величин (наприклад, 5π/6) Вивчіть і запам'ятайте значення тригонометричних функцій для особливих кутів.для визначення їх величин ви повинні поглянути на одиничну окружність. Згадайте про відрізку відомої довжини, укладеному в одиничної окружності. Точка на окружності відповідає кількості радіан в утвореному вугіллі. Наприклад, куту π/2 відповідає точка на окружності, радіус до якої утворює з позитивним горизонтальним радіусом кут величиною π / 2. Для знаходження значення тригонометричної функції будь-якого кута визначаються координати точки, відповідної цьому куту. Гіпотенуза завжди дорівнює одиниці, оскільки вона є радіусом кола, і так як будь-яке число, поділене на 1, дорівнює самому собі, а протилежний катет дорівнює довжині уздовж осі Оу, звідси випливає, що значення синуса будь-якого кута-це координата Y відповідної точки на окружності. Значення косинуса можна знайти схожим чином. Косинус дорівнює довжині прилеглого катета, поділеної на довжину гіпотенузи; оскільки остання дорівнює одиниці, а довжина прилеглого катета дорівнює координаті x точки на окружності, звідси випливає, що косинус дорівнює значенню цієї координати. Знайти тангенс трохи складніше. Тангенс кута прямокутного трикутника дорівнює протилежному катету, поділеному на прилеглий. В даному випадку, на відміну від попередніх, ПРИВАТНЕ не є константою, тому обчислення дещо ускладнюються. Згадаймо, що довжина протилежного катета дорівнює координаті y, а прилеглого-координаті x точки на одиничній окружності; підставивши ці значення, отримаємо, що тангенс дорівнює y/x. поділивши 1 на знайдені вище значення, можна легко знайти відповідні зворотні тригонометричні функції. Таким чином, можна розрахувати всі основні тригонометричні функції:
Вивчіть і запам'ятайте значення тригонометричних функцій для особливих кутів.для визначення їх величин ви повинні поглянути на одиничну окружність. Згадайте про відрізку відомої довжини, укладеному в одиничної окружності. Точка на окружності відповідає кількості радіан в утвореному вугіллі. Наприклад, куту π/2 відповідає точка на окружності, радіус до якої утворює з позитивним горизонтальним радіусом кут величиною π / 2. Для знаходження значення тригонометричної функції будь-якого кута визначаються координати точки, відповідної цьому куту. Гіпотенуза завжди дорівнює одиниці, оскільки вона є радіусом кола, і так як будь-яке число, поділене на 1, дорівнює самому собі, а протилежний катет дорівнює довжині уздовж осі Оу, звідси випливає, що значення синуса будь-якого кута-це координата Y відповідної точки на окружності. Значення косинуса можна знайти схожим чином. Косинус дорівнює довжині прилеглого катета, поділеної на довжину гіпотенузи; оскільки остання дорівнює одиниці, а довжина прилеглого катета дорівнює координаті x точки на окружності, звідси випливає, що косинус дорівнює значенню цієї координати. Знайти тангенс трохи складніше. Тангенс кута прямокутного трикутника дорівнює протилежному катету, поділеному на прилеглий. В даному випадку, на відміну від попередніх, ПРИВАТНЕ не є константою, тому обчислення дещо ускладнюються. Згадаймо, що довжина протилежного катета дорівнює координаті y, а прилеглого-координаті x точки на одиничній окружності; підставивши ці значення, отримаємо, що тангенс дорівнює y/x. поділивши 1 на знайдені вище значення, можна легко знайти відповідні зворотні тригонометричні функції. Таким чином, можна розрахувати всі основні тригонометричні функції:- Sinθ=y
- Cosθ=x
- Tgθ=y/x
- Cosec=1/y
- Sec=1/x
- Ctg=x/y
 Знайдіть і запам'ятайте значення шести тригонометричних функцій для кутів, що лежать на координатних осях, тобто кутів, кратних π/2, таких як 0, π/2, π, 3π/2, 2π і т. Д. для точок кола, що знаходяться на координатних осях, це не представляє ніяких проблем. Якщо точка лежить на осі Ох, синус дорівнює нулю, а косинус-1 або -1, в залежності від напрямку. Якщо ж точка лежить на осі Оу, синус буде дорівнювати 1 або -1, а косинус-0.
Знайдіть і запам'ятайте значення шести тригонометричних функцій для кутів, що лежать на координатних осях, тобто кутів, кратних π/2, таких як 0, π/2, π, 3π/2, 2π і т. Д. для точок кола, що знаходяться на координатних осях, це не представляє ніяких проблем. Якщо точка лежить на осі Ох, синус дорівнює нулю, а косинус-1 або -1, в залежності від напрямку. Якщо ж точка лежить на осі Оу, синус буде дорівнювати 1 або -1, а косинус-0. Знайдіть і запам'ятайте значення 6 тригонометричних функцій для особливого кута π/6. нанесіть кут π / 6 на одиничну окружність. Ви знаєте, як знаходити довжини всіх сторін особливих прямокутних трикутників (з кутами 30-60-90 і 45-45-90) по відомій довжині однієї зі сторін, а оскільки π/6=30 градусів, даний трикутник є одним з особливих випадків. Для нього, як ви пам'ятаєте, короткий катет дорівнює 1/2 гіпотенузи, тобто координата y становить 1/2, а довгий катет довший короткого в √3 разів, тобто дорівнює (√3)/2, так що координата x буде (√3) / 2. Таким чином, отримуємо точку на одиничній окружності з наступними координатами: ((√3)/2,1/2). Користуючись наведеними вище рівностями, знаходимо:
Знайдіть і запам'ятайте значення 6 тригонометричних функцій для особливого кута π/6. нанесіть кут π / 6 на одиничну окружність. Ви знаєте, як знаходити довжини всіх сторін особливих прямокутних трикутників (з кутами 30-60-90 і 45-45-90) по відомій довжині однієї зі сторін, а оскільки π/6=30 градусів, даний трикутник є одним з особливих випадків. Для нього, як ви пам'ятаєте, короткий катет дорівнює 1/2 гіпотенузи, тобто координата y становить 1/2, а довгий катет довший короткого в √3 разів, тобто дорівнює (√3)/2, так що координата x буде (√3) / 2. Таким чином, отримуємо точку на одиничній окружності з наступними координатами: ((√3)/2,1/2). Користуючись наведеними вище рівностями, знаходимо:- Sinπ/6=1/2
- Cosπ/6=(√3)/2
- Tgπ/6=1/(√3)
- Cosecπ/6=2
- Secπ/6=2/(√3)
- Ctgπ/6=√3
 Знайдіть і запам'ятайте значення 6 тригонометричних функцій для особливого кута π/3. кут π/3 відображається на окружності точкою, у якій координата x дорівнює координаті y кута π / 6, а координата y така ж, як x для цього кута. Таким чином, точка має координати (1/2, √3/2). В результаті отримуємо:
Знайдіть і запам'ятайте значення 6 тригонометричних функцій для особливого кута π/3. кут π/3 відображається на окружності точкою, у якій координата x дорівнює координаті y кута π / 6, а координата y така ж, як x для цього кута. Таким чином, точка має координати (1/2, √3/2). В результаті отримуємо:- Sinπ/3=(√3)/2
- Cosπ/3=1/2
- Tgπ/3=√3
- Cosecπ/3=2/(√3)
- Secπ/3=2
- Ctgπ/3=1/(√3)
 Знайдіть і запам'ятайте значення 6 тригонометричних функцій для особливого кута π/4. довжина гіпотенузи прямокутного трикутника з кутами 45-45-90 відноситься до довжин його катетів як √2 до 1, так само будуть співвідноситися і значення координат точки на одиничній окружності. У підсумку маємо:
Знайдіть і запам'ятайте значення 6 тригонометричних функцій для особливого кута π/4. довжина гіпотенузи прямокутного трикутника з кутами 45-45-90 відноситься до довжин його катетів як √2 до 1, так само будуть співвідноситися і значення координат точки на одиничній окружності. У підсумку маємо:- Sinπ/4=1/(√2)
- Cosπ/4=1/(√2)
- Tgπ/4=1
- Cosecπ/4=√2
- Secπ/4=√2
- Ctgπ/4=1
 Використовуйте правильне значення кута.ви вже знайшли значення основних тригонометричних функцій для трьох особливих кутів, але зробили це лише для першого квадранта. Якщо вам необхідно обчислити значення функцій для більшого або меншого кута, спочатку визначте, до якого "сімейства" належить даний кут. Наприклад, кут π/3 входить в ту ж сімейство, що і кути 2π/3, 4π/3 і 5π / 3. Загальне правило при цьому полягає в тому, щоб якомога більше скоротити чисельник і знаменник, а потім подивитися на Значення знаменника.
Використовуйте правильне значення кута.ви вже знайшли значення основних тригонометричних функцій для трьох особливих кутів, але зробили це лише для першого квадранта. Якщо вам необхідно обчислити значення функцій для більшого або меншого кута, спочатку визначте, до якого "сімейства" належить даний кут. Наприклад, кут π/3 входить в ту ж сімейство, що і кути 2π/3, 4π/3 і 5π / 3. Загальне правило при цьому полягає в тому, щоб якомога більше скоротити чисельник і знаменник, а потім подивитися на Значення знаменника.- Якщо воно дорівнює 3, кут відноситься до сімейства π / 3
- Якщо 6, то до сімейства π / 6
- Якщо 2 -- до сімейства π/2
- Якщо знаменник скоротився повністю, наприклад залишилося π або 0, кут належить до сімейства π
- Якщо 4, то це сімейство π/4
 Визначте, позитивно чи негативно значення функції.всі кути, що належать одному сімейству, дають однакові абсолютні значення тригонометричних функцій, але ці значення можуть відрізнятися за знаком (одне бути позитивним, друге-негативним).
Визначте, позитивно чи негативно значення функції.всі кути, що належать одному сімейству, дають однакові абсолютні значення тригонометричних функцій, але ці значення можуть відрізнятися за знаком (одне бути позитивним, друге-негативним).- Якщо Кут знаходиться в першому квадранті, всі тригонометричні функції мають позитивні значення.
- Для кута в другому квадранті всі функції, за винятком sin і cosec, негативні.
- У третьому квадранті значення всіх функцій, крім tg і ctg, менше нуля.
- У четвертому квадранті всі функції, за винятком cos і sec, мають негативні значення.