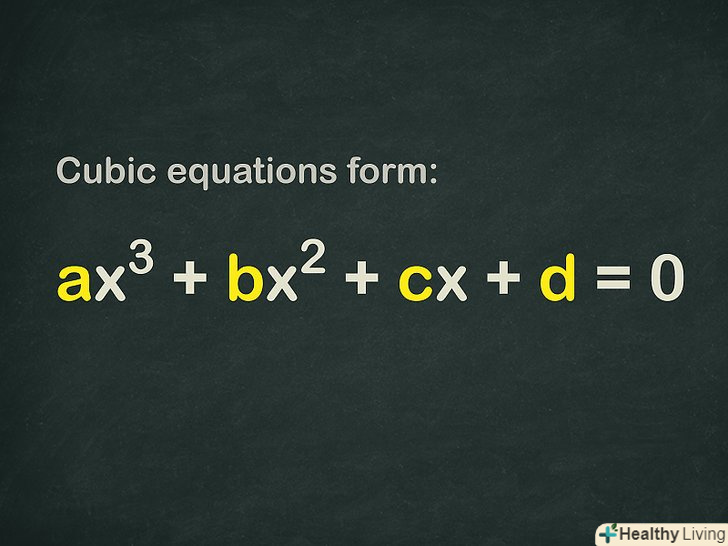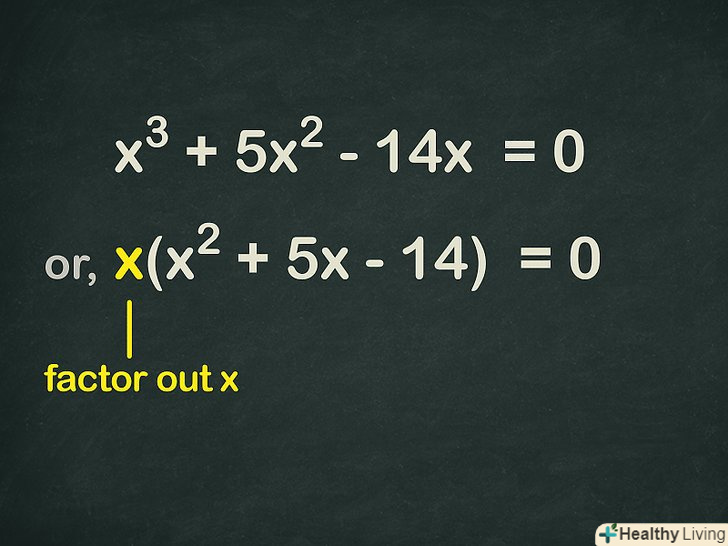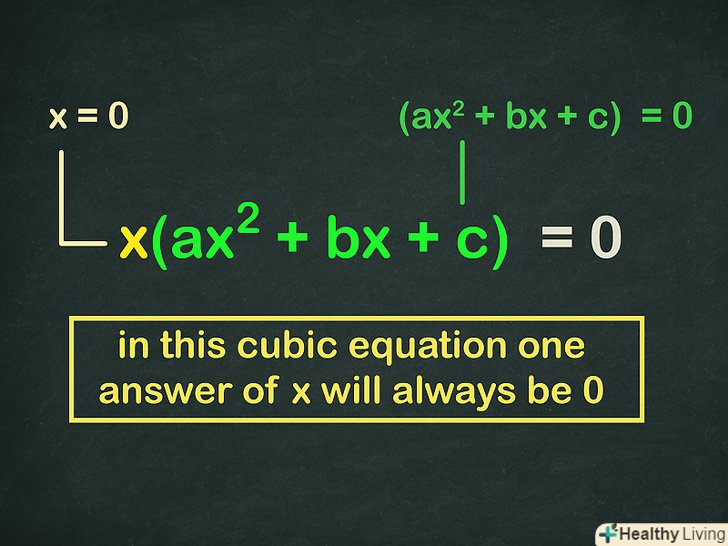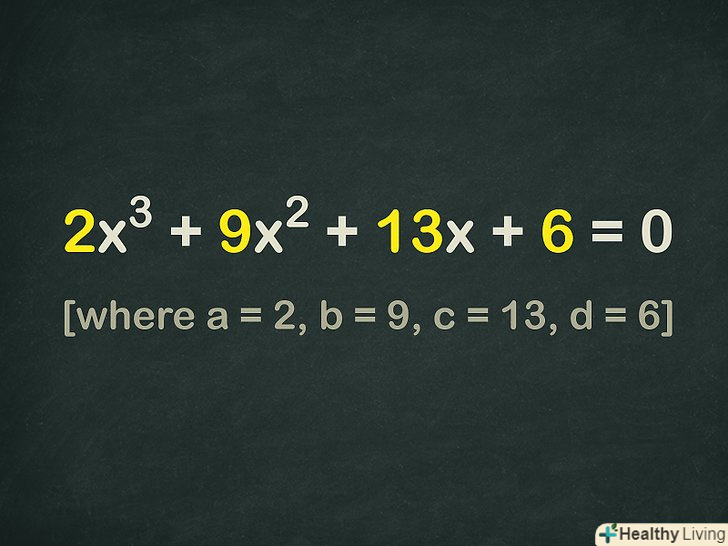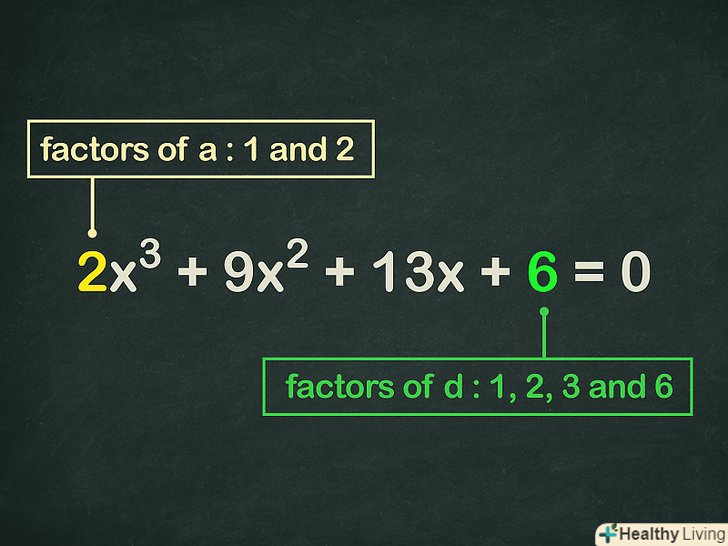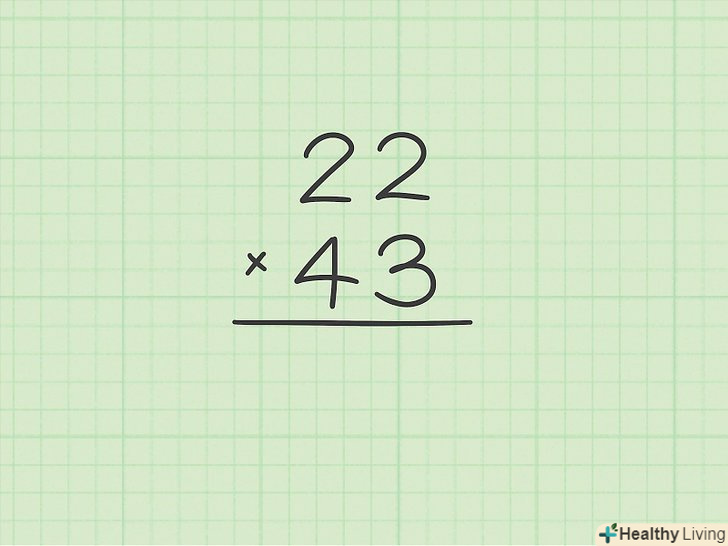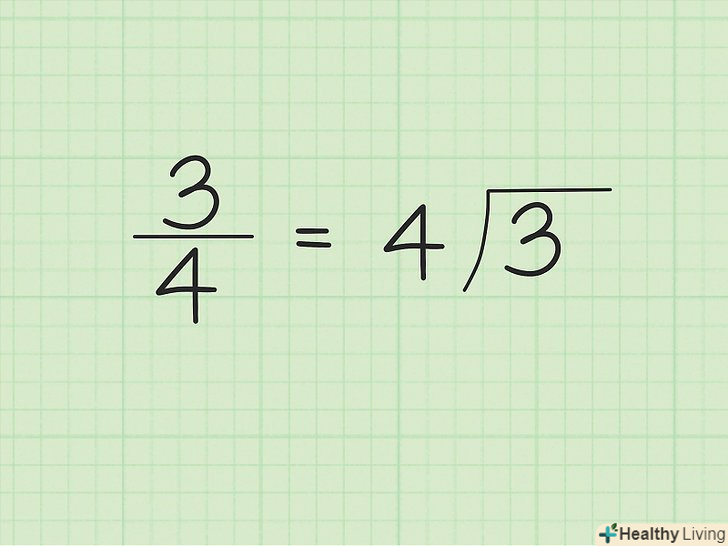В кубічному рівнянні найвищим показником ступеня є 3, у такого рівняння 3 кореня (рішення) і воно має вигляд. Деякі кубічні рівняння не так просто вирішити, але якщо застосувати правильний метод (при хорошій теоретичній підготовці), можна знайти коріння навіть найскладнішого кубічного рівняння — для цього скористайтеся формулою для вирішення квадратного рівняння, знайдіть цілі корені або обчисліть дискримінант.
Кроки
Метод1З 3:
Як вирішити кубічне рівняння без вільного члена
Метод1З 3:
 З'ясуйте, чи є в кубічному рівнянні вільний член
З'ясуйте, чи є в кубічному рівнянні вільний член. кубічне рівняння має вигляд
. Щоб рівняння вважалося кубічним, достатньо, щоб в ньому був присутній тільки член
(тобто інших членів може взагалі не бути).[1]
- Якщо в рівнянні є вільний член
, скористайтеся іншим методом.
- Якщо в рівнянні
, воно не є кубічним.[2]
- Якщо в рівнянні є вільний член
 Винесіть за дужки
Винесіть за дужки.оскільки в рівнянні немає вільного члена, кожен член рівняння включає змінну
. Це означає, що один
можна винести за дужки, щоб спростити рівняння. Таким чином, рівняння запишеться так:
.[3]
- Наприклад, дано кубічне рівняння
за дужки та отримайте
- Наприклад, дано кубічне рівняння
 Розкладіть на множники (на добуток двох біномів) квадратне рівняння (якщо можливо). багато квадратні рівняння виду
Розкладіть на множники (на добуток двох біномів) квадратне рівняння (якщо можливо). багато квадратні рівняння видуможна розкласти на множники. Таке рівняння вийде, якщо винести
за дужки. У нашому прикладі: [4]
- Винесіть за дужки
:
- Розкладіть на множники квадратне рівняння:
- Кожен біном приравняйте до
. Корінням даного рівняння є
.
- Винесіть за дужки
 Вирішіть квадратне рівняння за допомогою спеціальної формули.зробіть це, якщо квадратне рівняння не можна розкласти на множники. Щоб знайти два кореня рівняння, значення коефіцієнтів
Вирішіть квадратне рівняння за допомогою спеціальної формули.зробіть це, якщо квадратне рівняння не можна розкласти на множники. Щоб знайти два кореня рівняння, значення коефіцієнтів,
,
підставте в формулу
.[5]
- У нашому прикладі підставте значення коефіцієнтів
,
,
(
,
,
) у формулу:
- Перший корінь:
- Другий корінь:
- У нашому прикладі підставте значення коефіцієнтів
 Використовуйте нуль і коріння квадратного рівняння як рішення кубічного рівняння.у квадратних рівнянь два корені, а у кубічних — три. Два рішення Ви вже знайшли-це коріння квадратного рівняння. Якщо ж ви винесли» х "за дужки, третім рішенням буде
Використовуйте нуль і коріння квадратного рівняння як рішення кубічного рівняння.у квадратних рівнянь два корені, а у кубічних — три. Два рішення Ви вже знайшли-це коріння квадратного рівняння. Якщо ж ви винесли» х "за дужки, третім рішенням буде.[6]
- Якщо винести " х "за дужки, вийде
, тобто два множники:
і квадратне рівняння в дужках. Якщо будь-який з цих множників дорівнює
, всі рівняння також одно
.
- Таким чином, два кореня квадратного рівняння, є рішеннями кубічного рівняння. Третім рішенням є
.
- Якщо винести " х "за дужки, вийде
Метод2 З 3:
Як знайти цілі корені за допомогою множників
Метод2 З 3:
 Переконайтеся, що в кубічному рівнянні є вільний член
Переконайтеся, що в кубічному рівнянні є вільний член. якщо в рівнянні виду
є вільний член
(який не дорівнює нулю), винести «х» за дужки не вийде. В даному випадку скористайтеся методом, викладеним в цьому розділі.[7]
- Наприклад, дано кубічне рівняння
. Щоб на правій стороні рівняння отримати нуль, додайте
до обох сторін рівняння.
- Вийде рівняння
. Так як
, методом, який викладений в першому розділі, скористатися не вийде.
- Наприклад, дано кубічне рівняння
 Випишіть множники коефіцієнта
Випишіть множники коефіцієнтаі вільного члена
. тобто знайдіть множники числа при
і числа перед знаком рівності. Нагадаємо, що множниками числа є числа, при перемноженні яких виходить це число.[8]
- Наприклад, щоб отримати число6, потрібно перемножити
і
. Таким чином, числа 1, 2, 3, 6є множниками числа 6.
- У нашому рівнянні
і
. Множниками 2є1і2. Множниками 6є числа1,2,3і6.
- Наприклад, щоб отримати число6, потрібно перемножити
 Розділіть кожен множник
Розділіть кожен множникна кожен множник
.у підсумку вийде безліч дробів і кілька цілих чисел; корінням кубічного рівняння буде одне з цілих чисел або негативне значення одного з цілих чисел.[9]
- У нашому прикладі розділіть множники
(1 та 2) на множники
(1, 2, 3 і 6). Ви отримаєте:
,
,
,
,
і
. Тепер в цей список додайте негативні значення отриманих дробів і чисел:
,
,
,
,
,
,
,
,
- У нашому прикладі розділіть множники