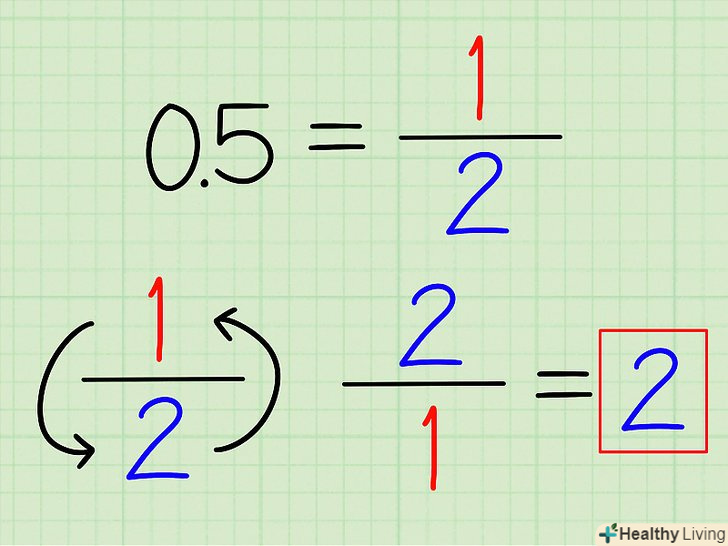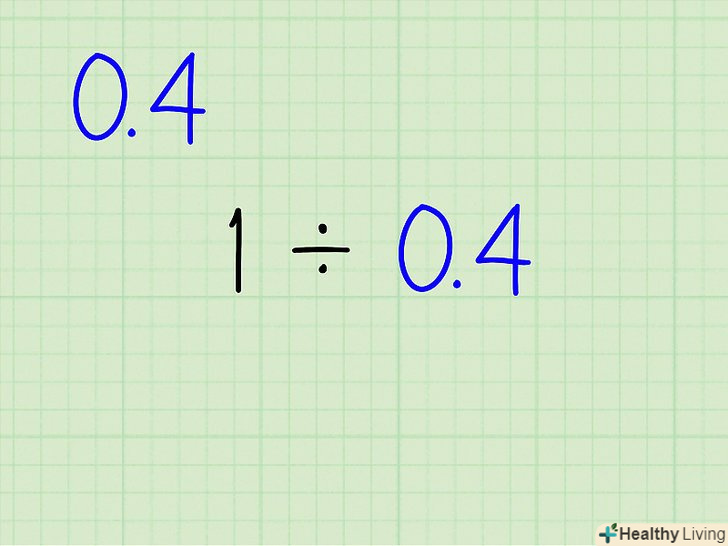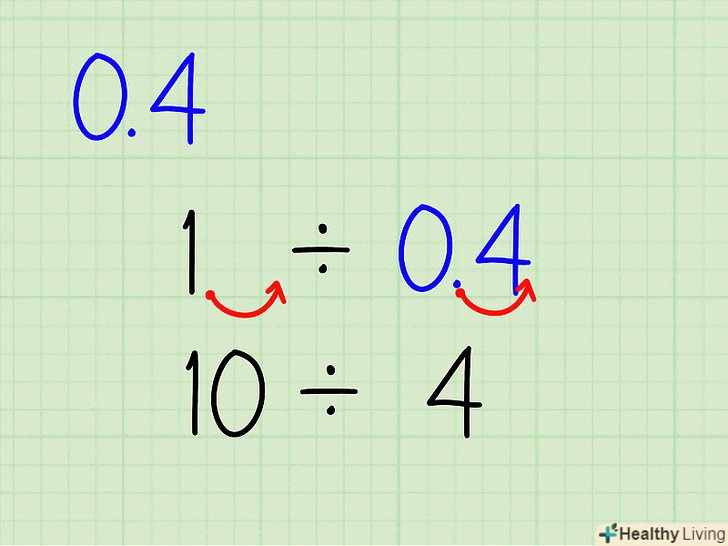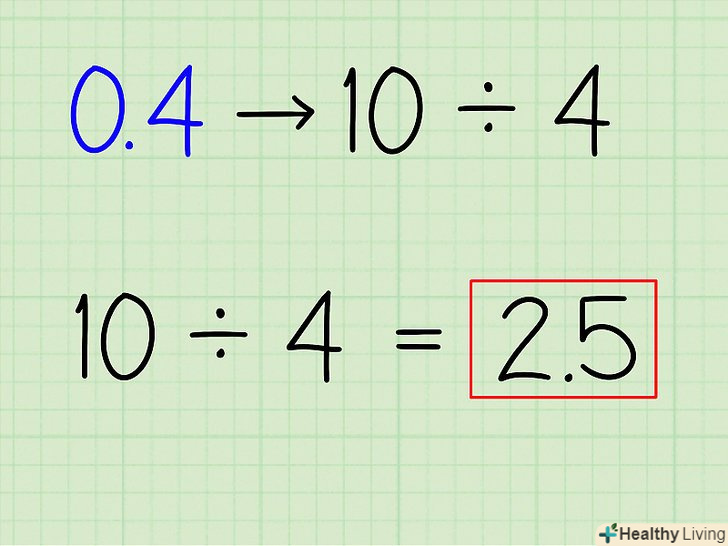Зворотні числа потрібні при розв'язанні всіх типів алгебраїчних рівнянь. Наприклад, якщо вам потрібно розділити одне дробове число на інше, ви множите перше число на зворотне число другого. Крім того, Зворотні числа застосовують при знаходженні рівняння прямої.
Кроки
Метод1З 3:
Знаходження зворотного числа для дробу або цілого числа
Метод1З 3:
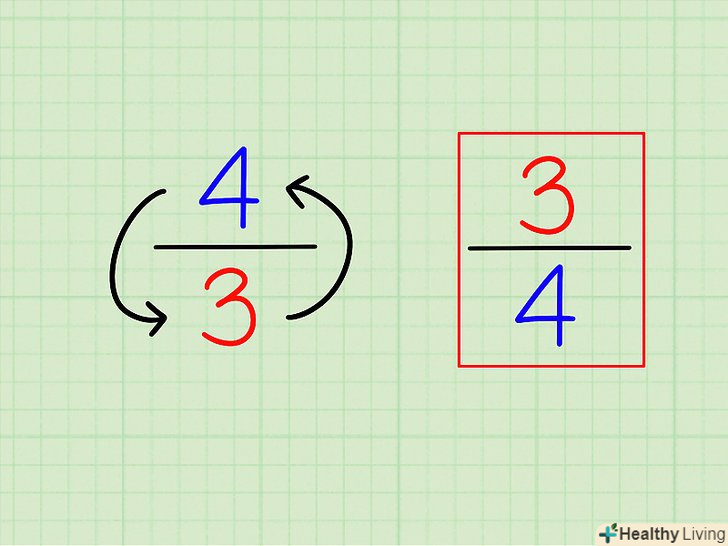
 Знайдіть зворотне число для дробового числа, перевернувши його. "зворотне число" визначається дуже просто. Щоб обчислити його, просто розрахуйте значення виразу " 1 ÷ (вихідне число)."Для дробового числа зворотним числом є інше дробове число, яке можна обчислити просто "перевернувши" дріб (помінявши місцями чисельник і знаменник).[1]
Знайдіть зворотне число для дробового числа, перевернувши його. "зворотне число" визначається дуже просто. Щоб обчислити його, просто розрахуйте значення виразу " 1 ÷ (вихідне число)."Для дробового числа зворотним числом є інше дробове число, яке можна обчислити просто "перевернувши" дріб (помінявши місцями чисельник і знаменник).[1]- Наприклад, зворотним числом дробу3/4 є4/3 .
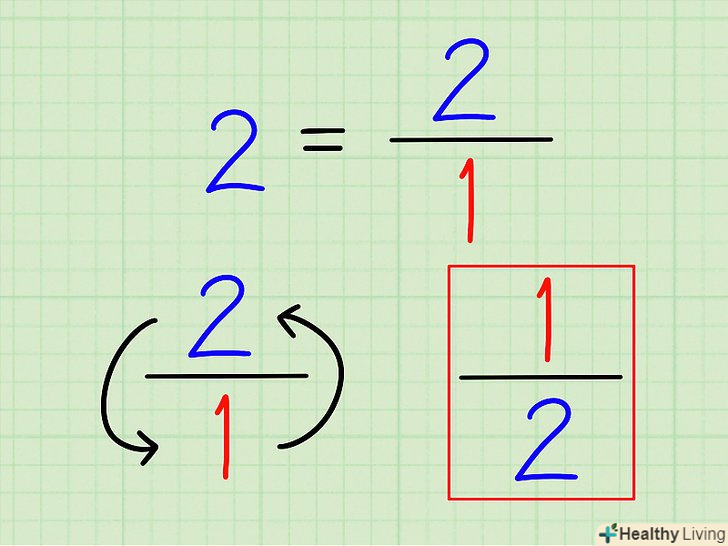
 Запишіть зворотне число для цілого числа у вигляді дробу.і в цьому випадку зворотне число обчислюється, як 1 ÷ (вихідне число). Для цілого числа запишіть зворотне число у вигляді звичайного дробу, не потрібно проводити обчислення і записувати його у вигляді десяткового дробу.
Запишіть зворотне число для цілого числа у вигляді дробу.і в цьому випадку зворотне число обчислюється, як 1 ÷ (вихідне число). Для цілого числа запишіть зворотне число у вигляді звичайного дробу, не потрібно проводити обчислення і записувати його у вигляді десяткового дробу.- Наприклад, зворотне число для 2 дорівнює 1 ÷ 2 =1/2.
Метод2 З 3:
Знаходження зворотного числа змішаного дробу
Метод2 З 3:
 Що таке "змішаний дріб". змішаним дробом називається число, записане у вигляді цілого числа і простий дробу, наприклад, 24/5. Знаходження зворотного числа для змішаного дробу здійснюється в два етапи, описаних нижче.
Що таке "змішаний дріб". змішаним дробом називається число, записане у вигляді цілого числа і простий дробу, наприклад, 24/5. Знаходження зворотного числа для змішаного дробу здійснюється в два етапи, описаних нижче. Запишіть змішаний дріб у вигляді неправильного дробу. ви, звичайно, пам'ятаєте, що одиниця може бути записана у вигляді(число)/(те ж число), а дроби з однаковим знаменників (числом під рисою) можна скласти один з одним. Ось як це можна зробити для дробу 24 / 5:
Запишіть змішаний дріб у вигляді неправильного дробу. ви, звичайно, пам'ятаєте, що одиниця може бути записана у вигляді(число)/(те ж число), а дроби з однаковим знаменників (числом під рисою) можна скласти один з одним. Ось як це можна зробити для дробу 24 / 5:- 24/5
- = 1 + 1 +4/5
- =5/5 + 5/5 + 4/5
- =(5+5+4)/5
- =14/5.
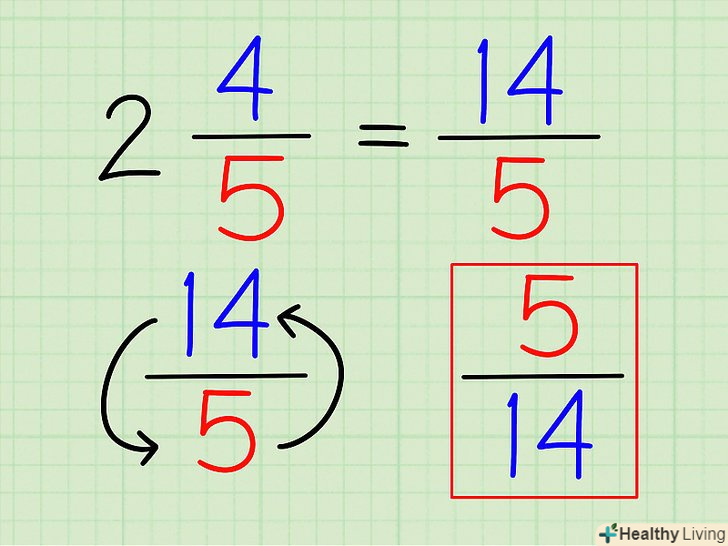
 Переверніть дріб. коли змішана дріб записана у вигляді неправильної дробу, ми можемо легко знайти зворотне число, просто помінявши місцями чисельник і знаменник.
Переверніть дріб. коли змішана дріб записана у вигляді неправильної дробу, ми можемо легко знайти зворотне число, просто помінявши місцями чисельник і знаменник.- Для наведеного вище прикладу зворотне число дорівнюватиме14/5 - 5/14.
Метод3 З 3:
Знаходження зворотного числа для десяткового дробу
Метод3 З 3:
 Якщо це можливо, висловіть десятковий дріб у вигляді простого дробу. вам потрібно знати, що багато десяткових дробів можна легко перетворити на прості дроби. Наприклад, 0,5 = 1/2, а 0,25 = 1/4. Коли ви записали число у вигляді простого дробу, то зможете легко знайти зворотне число, просто перевернувши дріб.
Якщо це можливо, висловіть десятковий дріб у вигляді простого дробу. вам потрібно знати, що багато десяткових дробів можна легко перетворити на прості дроби. Наприклад, 0,5 = 1/2, а 0,25 = 1/4. Коли ви записали число у вигляді простого дробу, то зможете легко знайти зворотне число, просто перевернувши дріб.- Наприклад, зворотне число для 0,5 дорівнює2/1 = 2.
 Вирішіть задачу за допомогою ділення.якщо ви не можете записати десятковий дріб у вигляді простого дробу, розрахуйте зворотне число, вирішивши задачу діленням: 1 ÷ (десятковий дріб). Для вирішення Ви можете скористатися калькулятором або перейти до наступного кроку, якщо хочете розрахувати значення вручну.
Вирішіть задачу за допомогою ділення.якщо ви не можете записати десятковий дріб у вигляді простого дробу, розрахуйте зворотне число, вирішивши задачу діленням: 1 ÷ (десятковий дріб). Для вирішення Ви можете скористатися калькулятором або перейти до наступного кроку, якщо хочете розрахувати значення вручну.- Наприклад, зворотне число для 0,4 розраховується як 1 ÷ 0,4.
 Змініть вираз, щоб працювати з цілими числами.перший крок у діленні десяткового дробу-це переміщення позиційної коми до тих пір, поки всі числа у виразі не стануть цілими числами. Оскільки ви переміщуєте позиційну кому на однакову кількість знаків, як в діленому, так і в дільнику, Ви отримуєте правильну відповідь.
Змініть вираз, щоб працювати з цілими числами.перший крок у діленні десяткового дробу-це переміщення позиційної коми до тих пір, поки всі числа у виразі не стануть цілими числами. Оскільки ви переміщуєте позиційну кому на однакову кількість знаків, як в діленому, так і в дільнику, Ви отримуєте правильну відповідь.- Наприклад, ви берете вираз 1 ÷ 0,4 і записуєте його як 10 ÷ 4. У цьому випадку ви перемістили кому на один знак вправо, що рівносильно тому, якби ви помножили кожне число на десять.
 Вирішіть задачу, розділивши числа стовпчиком.за допомогою ділення стовпчиком ви зможете розрахувати зворотне число. Якщо ви розділите 10 на 4, у вас повинно вийти 2,5, що і буде зворотним числом для 0,4.
Вирішіть задачу, розділивши числа стовпчиком.за допомогою ділення стовпчиком ви зможете розрахувати зворотне число. Якщо ви розділите 10 на 4, у вас повинно вийти 2,5, що і буде зворотним числом для 0,4.
Поради
- Значення негативного зворотного числа дорівнюватиме зворотному числу, помноженому на -1.[2] наприклад, негативне зворотне число для 3/4 дорівнює -4/3.
- Зворотне число іноді називають "зворотним значенням"або" зворотною величиною".[3]
- Число 1 є своїм власним зворотним числом, оскільки 1 ÷ 1 = 1.
- Нуль не має зворотного числа, оскільки вираз 1 ÷ 0 не має рішень.[4]