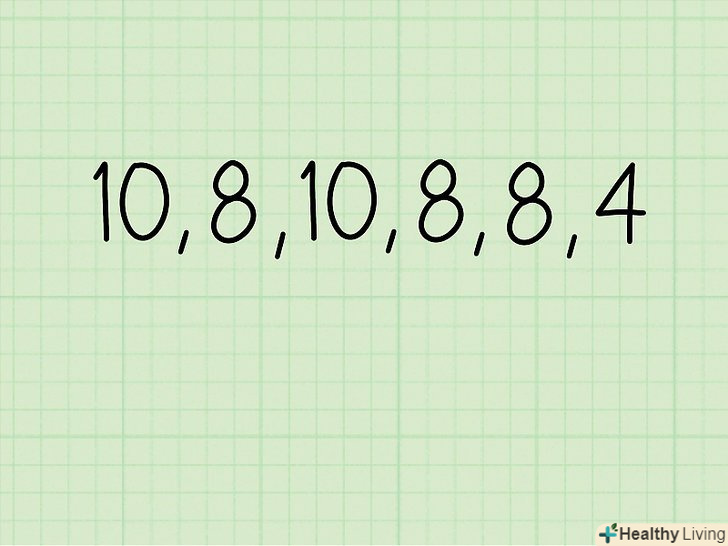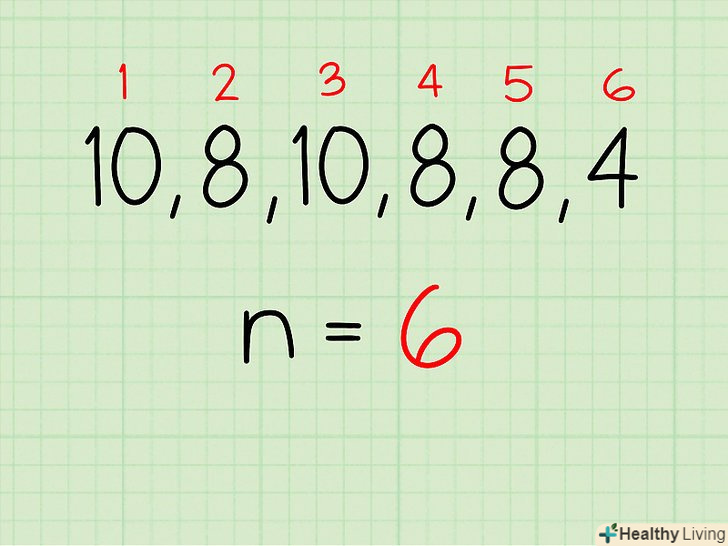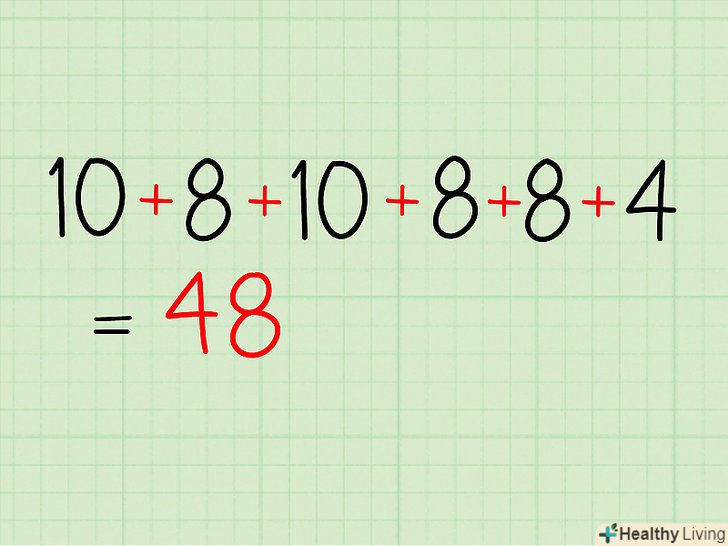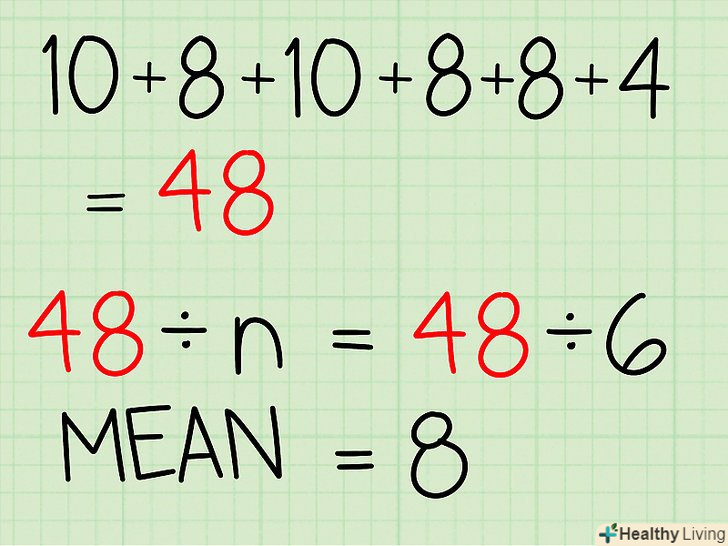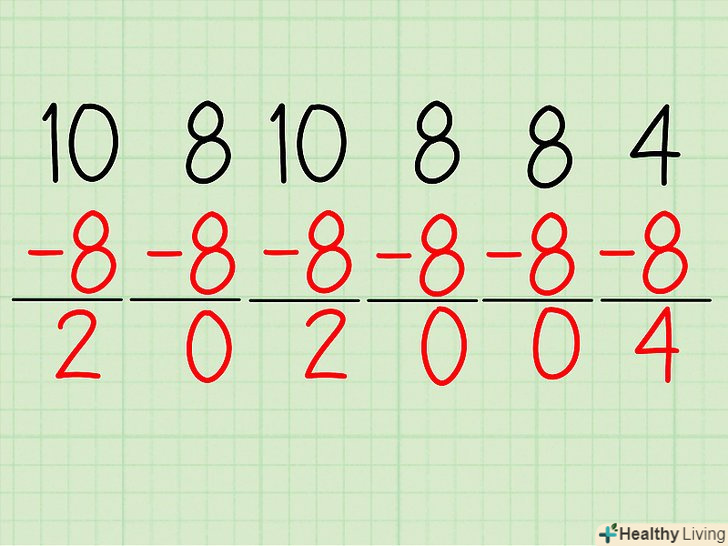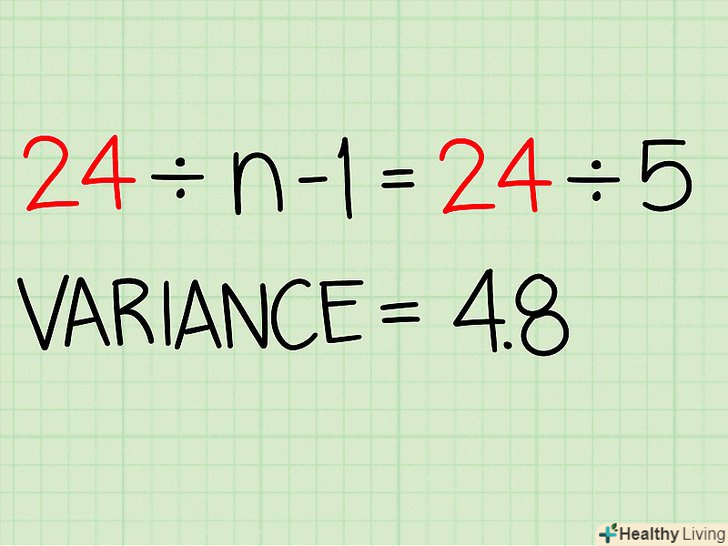Обчисливши середньоквадратичне відхилення, ви знайдете розкид значень у вибірці даних.[1] але спочатку вам доведеться обчислити деякі величини: середнє значення і дисперсію вибірки. Дисперсія-міра розкиду даних навколо середнього значення.[2] середньоквадратичне відхилення дорівнює квадратному кореню з дисперсії вибірки. Ця стаття розповість вам, як знайти середнє значення, дисперсію і середньоквадратичне відхилення.
Кроки
Частина1З 3:
Середнє значення
Частина1З 3:
Візьміть набір даних. середнє значення-це важлива величина в статистичних розрахунках.[3]- Визначте кількість чисел у наборі даних.
- Числа в наборі сильно відрізняються один від одного або вони дуже близькі (відрізняються на дробові частки)?
- Що представляють числа в наборі даних? Тестові оцінки, показання пульсу, зростання, ваги і так далі.
- Наприклад, набір тестових оцінок: 10, 8, 10, 8, 8, 4.
-
Для обчислення середнього значення знадобляться всі числа даного набору даних.[4]
- Середнє значення-це усереднене значення всіх чисел в наборі даних.
- Для обчислення середнього значення складіть всі числа вашого набору даних і розділіть отримане значення на загальну кількість чисел в наборі (n).
- У нашому прикладі (10, 8, 10, 8, 8, 4) n = 6.
-
Складіть всі числа вашого набору даних.[5]
- У нашому прикладі дані числа: 10, 8, 10, 8, 8 і 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Це сума всіх чисел в наборі даних.
- Складіть числа ще раз, щоб перевірити відповідь.
-
Розділіть суму чисел на кількість чисел (n) у вибірці. Ви знайдете середнє значення.[6]
- У нашому прикладі (10, 8, 10, 8, 8 і 4) n = 6.
- У нашому прикладі сума чисел дорівнює 48. Таким чином, розділіть 48 на n.
- 48/6 = 8
- Середнє значення даної вибірки дорівнює 8.
Частина2З 3:
Дисперсія
Частина2З 3:
-
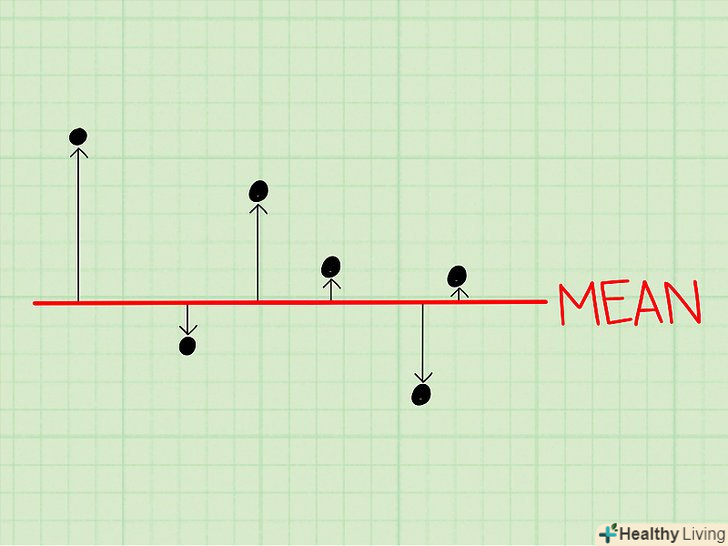
Обчисліть дисперсію. це міра розкиду даних навколо середнього значення.[7]
- Ця величина дасть вам уявлення про те, як розкидані дані вибірки.
- Вибірка з малою дисперсією включає дані, які ненабагато відрізняються від середнього значення.
- Вибірка з високою дисперсією включає дані, які сильно відрізняються від середнього значення.
- Дисперсію часто використовують для того, щоб порівняти розподіл двох наборів даних.
-
Відніміть середнє значення з кожного числа в наборі даних. ви дізнаєтеся, наскільки кожна величина в наборі даних відрізняється від середнього значення.[8]
- У нашому прикладі (10, 8, 10, 8, 8, 4) середнє значення дорівнює 8.
- 10 - 8 = 2; 8 - 8 = 0, 10 - 2 = 8, 8 - 8 = 0, 8 - 8 = 0, і 4-8 = -4.
- Виконайте віднімання ще раз, щоб перевірити кожну відповідь. Це дуже важливо, так як отримані значення знадобляться при обчисленнях інших величин.
-
Зведіть в квадрат кожне значення, отримане вами в попередньому кроці.[9]
- При відніманні середнього значення (8) з кожного числа даної вибірки (10, 8, 10, 8, 8 і 4) Ви отримали наступні значення: 2, 0, 2, 0, 0 і -4.
- Зведіть ці значення в квадрат: 22, 02, 22, 02, 02, і (-4)2 = 4, 0, 4, 0, 0, і 16.
- Перевірте відповіді, перш ніж приступити до наступного кроку.
-
Складіть квадрати значень, тобто знайдіть суму квадратів.[10]
- У нашому прикладі квадрати значень: 4, 0, 4, 0, 0 і 16.
- Нагадаємо, що значення отримані шляхом віднімання середнього значення з кожного числа вибірки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сума квадратів дорівнює 24.
-
Розділіть суму квадратів на (n-1).Пам'ятайте, що n-це кількість даних (чисел) у вашій вибірці. Таким чином, ви отримаєте дисперсію.[11]
- У нашому прикладі (10, 8, 10, 8, 8, 4) n = 6.
- N-1 = 5.
- У нашому прикладі сума квадратів дорівнює 24.
- 24/5 = 4,8
- Дисперсія даної вибірки дорівнює 4,8.
Частина3З 3:
Середньоквадратичне відхилення
Частина3З 3:
-
Знайдіть дисперсію, щоб обчислити середньоквадратичне відхилення.[12]
- Пам'ятайте, що дисперсія-це міра розкиду даних навколо середнього значення.
- Середньоквадратичне відхилення-це аналогічна величина, що описує характер розподілу даних у вибірці.
- У нашому прикладі дисперсія дорівнює 4,8.
-
Вийміть квадратний корінь з дисперсії, щоб знайти середньоквадратичне відхилення.[13]
- Як правило, 68% всіх даних розташовані в межах одного середньоквадратичного відхилення від середнього значення.
- У нашому прикладі дисперсія дорівнює 4,8.
- √4,8 = 2,19. Середньоквадратичне відхилення даної вибірки дорівнює 2,19.
- 5 з 6 чисел (83%) даної вибірки (10, 8, 10, 8, 8, 4) знаходиться в межах одного середньоквадратичного відхилення (2,19) від середнього значення (8).
-
Перевірте правильність обчислення середнього значення, дисперсії і середньоквадратичного відхилення.це дозволить вам перевірити вашу відповідь.[14]
- Обов'язково записуйте обчислення.
- Якщо в процесі перевірки обчислень ви отримали інше значення, перевірте всі обчислення з самого початку.
- Якщо ви не можете знайти, де зробили помилку, виконайте обчислення з самого початку.
Джерела
- ↑ Http://www.mathsisfun.com/data/standard-deviation.html
- ↑ Http://www.mathsisfun.com/data/standard-deviation.html
- ↑ Http://www.mathsisfun.com/data/standard-deviation.html
- ↑ Http://www.mathsisfun.com/data/standard-deviation.html
- ↑ Http://www.mathsisfun.com/data/standard-deviation.html
- ↑ Http://www.mathsisfun.com/data/standard-deviation.html
- ↑ Http://pirate.shu.edu/~wachsmut/Teaching/MATH1101/Descriptives/variability.html
- ↑ Http://pirate.shu.edu/~wachsmut/Teaching/MATH1101/Descriptives/variability.html
- ↑ Http://pirate.shu.edu/~wachsmut/Teaching/MATH1101/Descriptives/variability.html
- ↑ Http://pirate.shu.edu/~wachsmut/Teaching/MATH1101/Descriptives/variability.html
- ↑ Http://pirate.shu.edu/~wachsmut/Teaching/MATH1101/Descriptives/variability.html
- ↑ Http://pirate.shu.edu/~wachsmut/Teaching/MATH1101/Descriptives/variability.html
- ↑ Http://pirate.shu.edu/~wachsmut/Teaching/MATH1101/Descriptives/variability.html
- ↑ Http://pirate.shu.edu/~wachsmut/Teaching/MATH1101/Descriptives/variability.html
