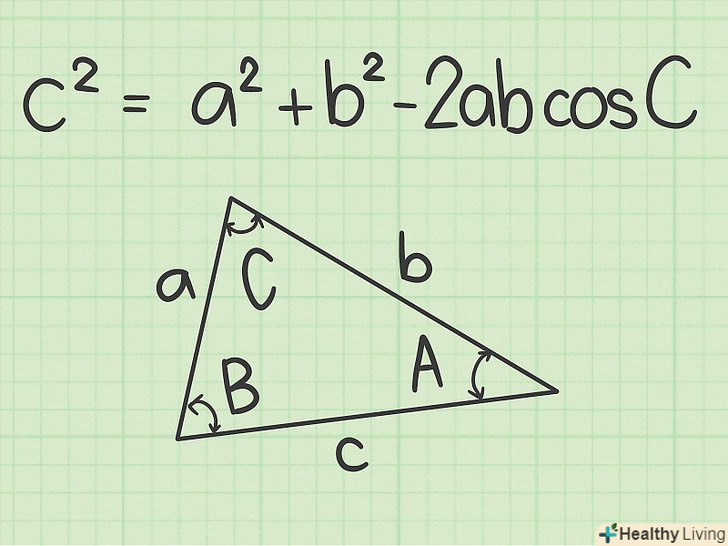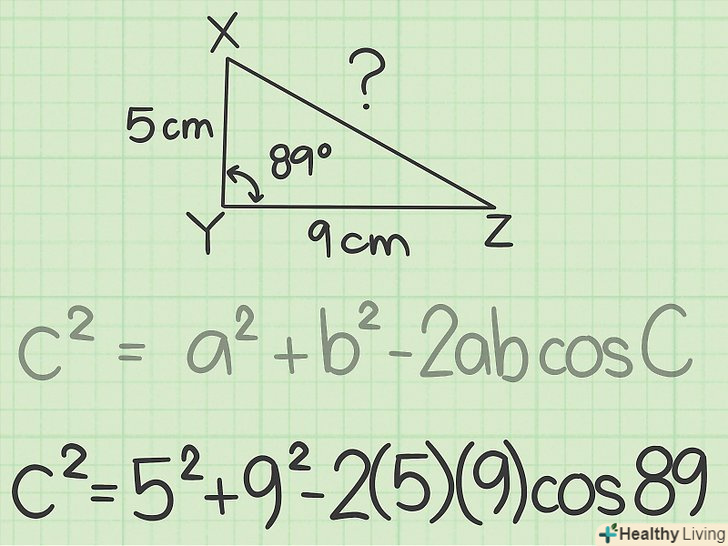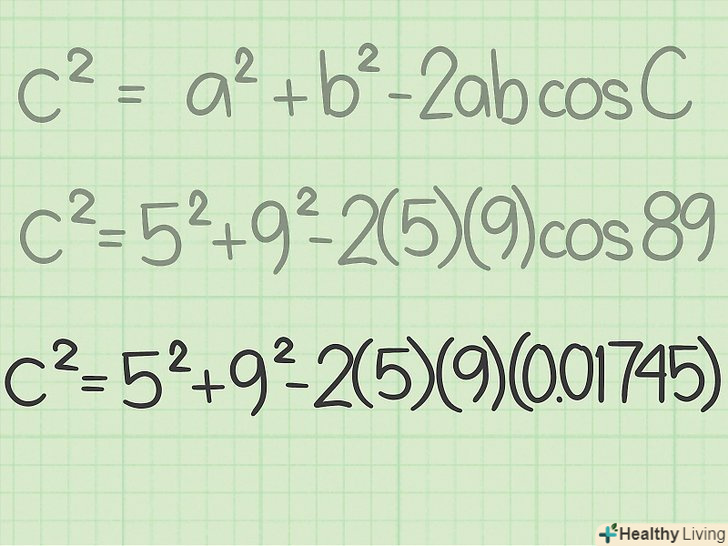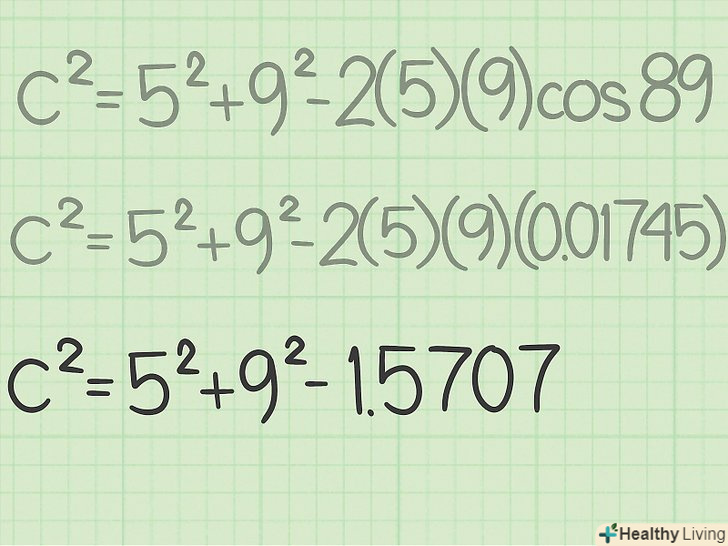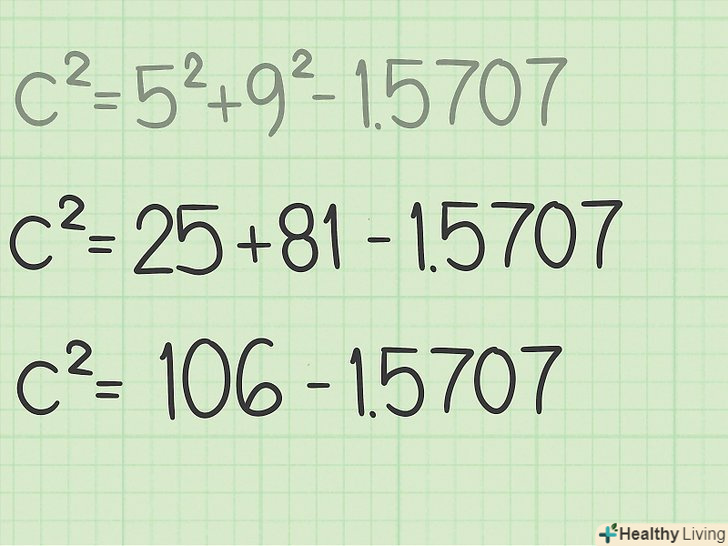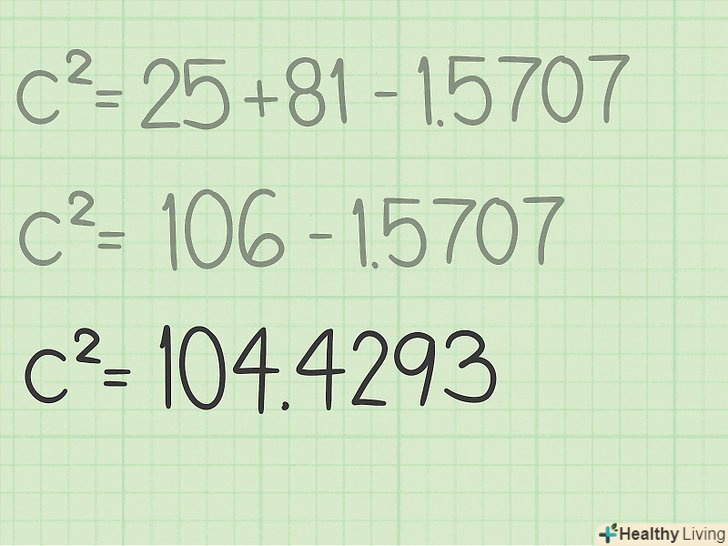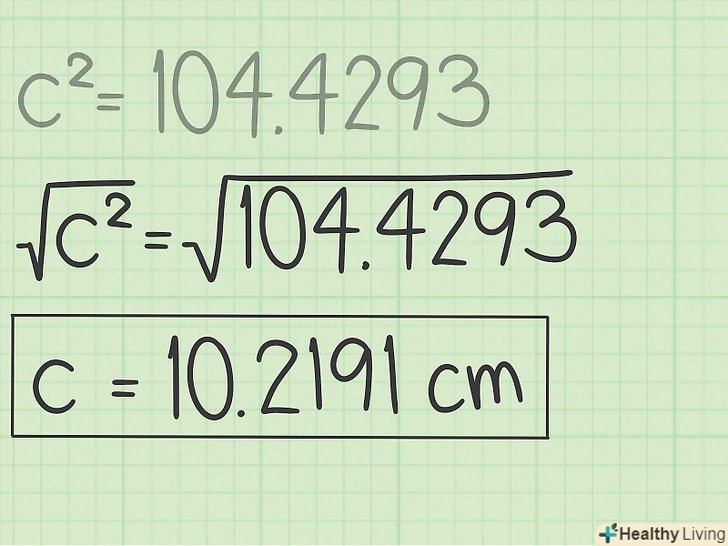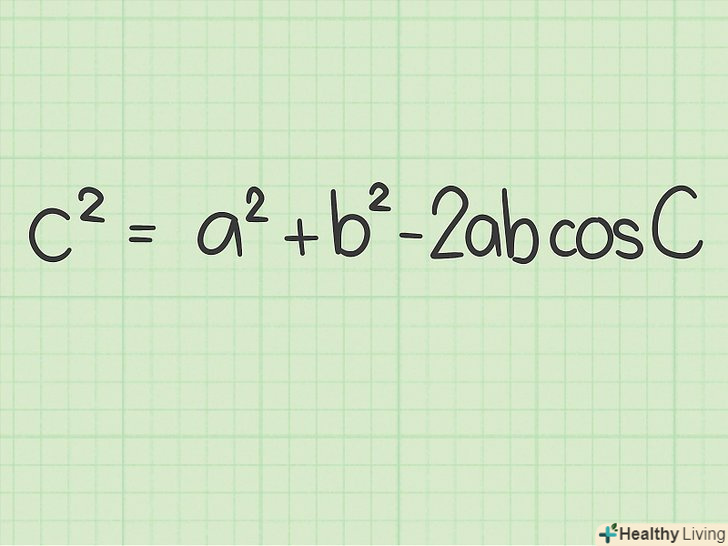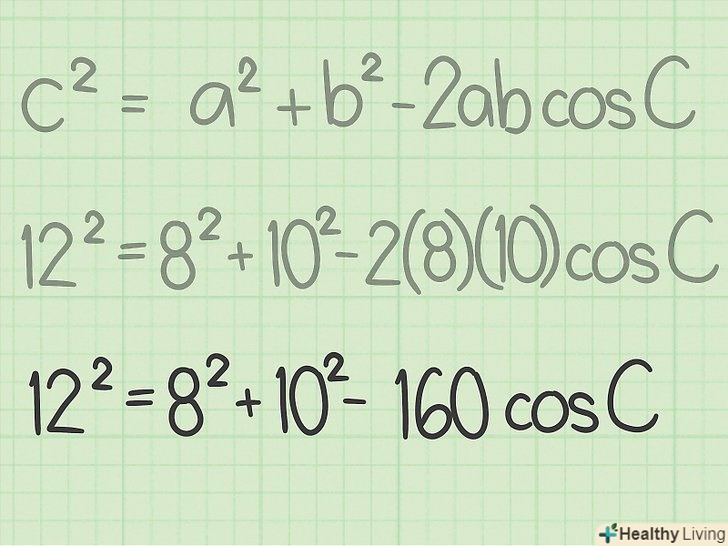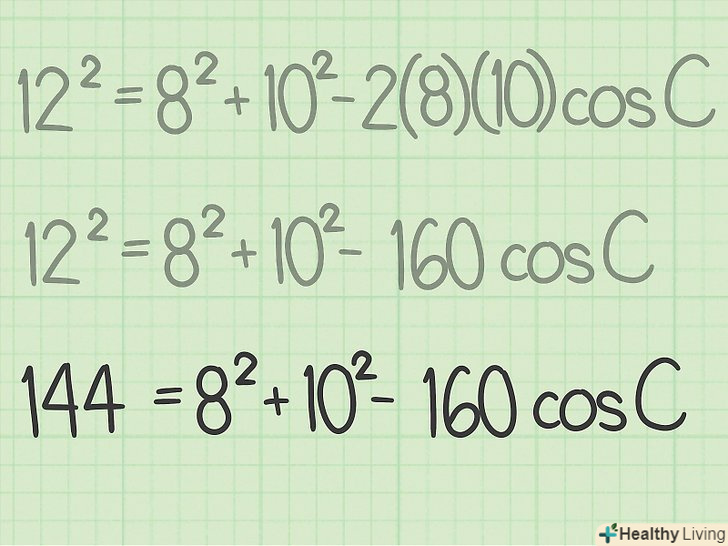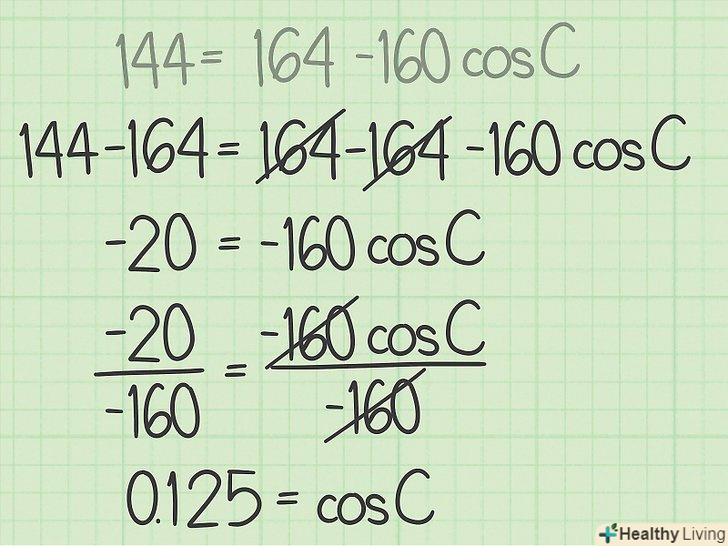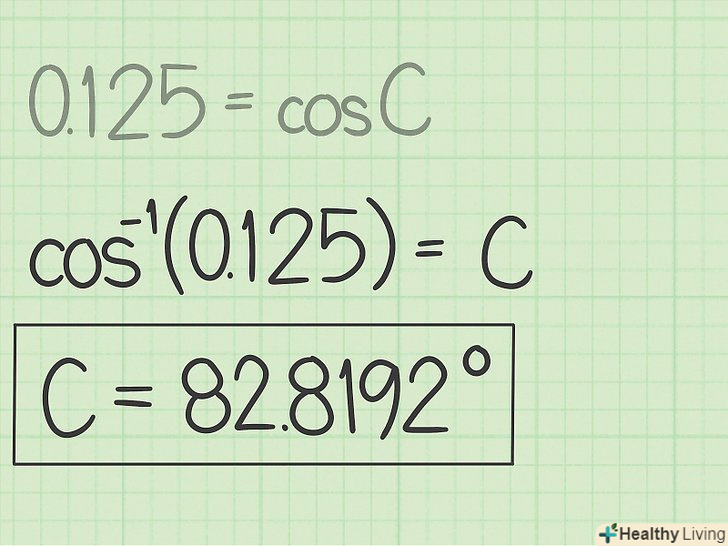1. Головна
    2. Геометрія
    3. Як користуватися теоремою косинусів-

Як користуватися теоремою косинусів-

Теорема косинусів широко застосовується втригонометрії. Її використовують при роботі з неправильними трикутниками, щоб знаходити невідомі величини, наприклад сторони і кути. Теорема схожа з теорема Піфагора, і її досить легко запам'ятати. Теорема косинусів говорить, що в будь-якому трикутнику C2=a2+b2−2abcos⁡C{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos {C}}.

Метод1З 3:
Як знайти невідому сторону

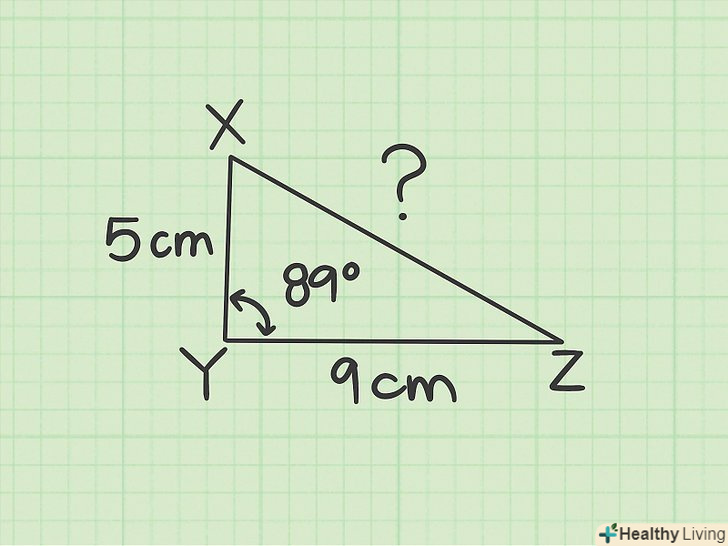
  1. Запишіть відомі величини.щоб знайти невідому сторону трикутника, потрібно знати дві інші сторони і кут між ними.[1]
    • Наприклад, дано трикутник XYZ. Сторона YX дорівнює 5 см, сторона YZ дорівнює 9 см, а кут Y дорівнює 89°. Чому дорівнює сторона XZ?
  2. Запишіть формулу теореми косинусів. Формула: C2=a2+b2−2abcos⁡C{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos {C}}, де — невідома сторона, Cos⁡C{\displaystyle \cos {C}} — косинус кута, протилежного невідомій стороні, A{\displaystyle a} і — дві відомі сторони.[2]
  3. Підставте відомі значення в формулу. змінні A{\displaystyle a} і позначають дві відомі сторони. Змінна C{\displaystyle C} — це відомий кут, який лежить між сторонами і .[3]
    • У нашому прикладі сторона XZ невідома, тому у формулі вона позначена якC{\displaystyle c}. Так як сторони YX і YZ відомі, вони позначені змінними A{\displaystyle a} і . Змінна C{\displaystyle C} — це кут Y. Отже, формула запишеться наступним чином: C2=52+92−2(5)(9)cos⁡89{\displaystyle c^{2}=5^{2}+9^{2}-2(5)(9)\cos {89}}.
  4. Знайдіть косинус відомого кута.зробіть це за допомогою калькулятора. Введіть значення кута, а потім натисніть кнопку COS{\displaystyle COS}. Якщо у вас немає наукового калькулятора, знайдіть онлайн-таблицю значень косинусів, наприклад, тут.[4] також в Яндексі можна ввести "косинус х градусів" (замість X підставте значення кута), і пошукова система відобразить косинус кута.
    • Наприклад, косинус 89° ≈ 0,01745. Отже:C2=52+92−2(5)(9)(0,01745){\displaystyle c^{2}=5^{2}+9^{2}-2(5)(9)(0,01745)}.
  5. Перемножьте числа. помножте 2ab{\displaystyle 2ab} на косинус відомого кута.
    • Наприклад:
      C2=52+92−2(5)(9)(0,01745){\displaystyle c^{2}=5^{2}+9^{2}-2(5)(9)(0,01745)}
  6. Складіть квадрати відомих сторін.Пам'ятайте, щоб звести число в квадрат, його потрібно помножити на саме себе. Спочатку зведіть в квадрат відповідні числа, а потім складіть отримані значення.
    • Наприклад:
      C2=52+92−1,5707{\displaystyle c^{2}=5^{2}+9^{2}-1,5707}

  7. Відніміть два числа. ви знайдете C2{\displaystyle c^{2}}.
    • Наприклад:
      C2=106−1,5707{\displaystyle c^{2}=106-1,5707}
  8. Витягніть квадратний корінь з отриманого значення.для цього скористайтеся калькулятором. Так ви знайдете невідому сторону.[5]
    • Наприклад:
      C2=104,4293{\displaystyle c^{2}=104,4293}


      Отже, невідома сторона дорівнює 10,2191 див.

Метод2 З 3:
Як знайти невідомий кут

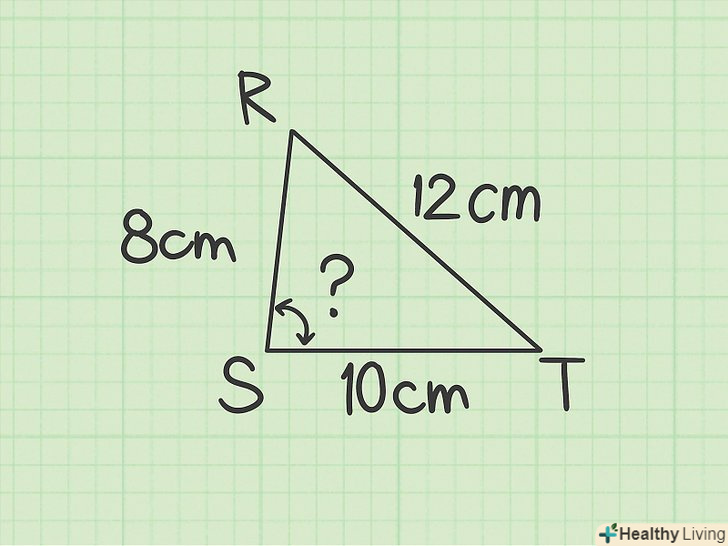
  1. Запишіть відомі величини.щоб знайти невідомий кут трикутника, потрібно знати всі три сторони трикутника.[6]
    • Наприклад, дано трикутник RST. Сторона СР = 8 см, ST = 10 см, РТ = 12 см. знайдіть значення кута S.
  2. Запишіть формулу теореми косинусів. Формула: C2=a2+b2−2abcos⁡C{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos {C}}, де — косинус невідомого кута, — відома сторона, протилежна невідомому куту, A{\displaystyle a} і — дві інші відомі сторони. [7]
  3. Знайдіть значенняA{\displaystyle a}, і .потім підставте їх у формулу.[8]
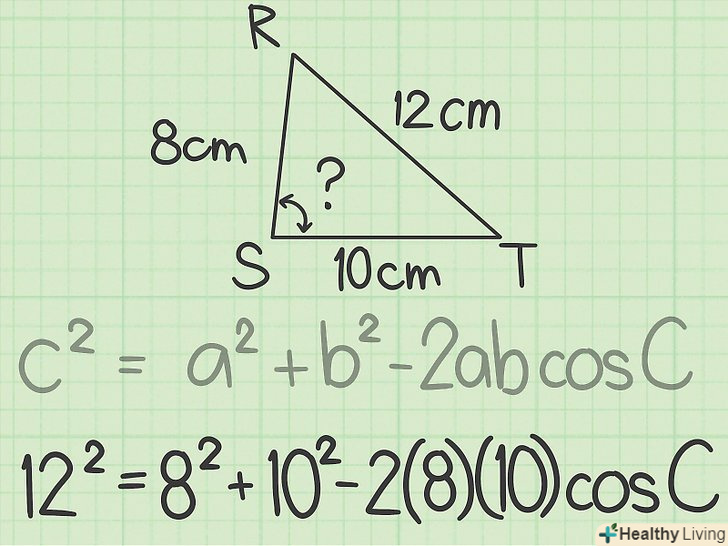
    • Наприклад, сторона RT протилежна невідомому куту S, тому сторона RT — це у формулі. Інші сторони будуть A{\displaystyle a} і . Отже, формула запишеться наступним чином: 122=82+102−2(8)(10)cos⁡C{\displaystyle 12^{2}=8^{2}+10^{2}-2(8)(10)\cos {C}}.
  4. Перемножьте числа. помножте 2ab{\displaystyle 2ab} на косинус невідомого кута.
    • Наприклад,122=82+102−160cos⁡C{\displaystyle 12^{2}=8^{2}+10^{2}-160\cos {C}}.
  5. ЗведітьC{\displaystyle c} в квадрат.тобто помножте число саме себе.
    • Наприклад,144=82+102−160cos⁡C{\displaystyle 144=8^{2}+10^{2}-160\cos {C}}
  6. Складіть квадратиA{\displaystyle a} і .але спочатку зведіть відповідні числа в квадрат.
    • Наприклад:
      144=64+100−160cos⁡C{\displaystyle 144=64+100-160\cos {C}}
  7. Ізолюйте косинус невідомого кута. Для цього відніміть суму і B2{\displaystyle b^{2}} з обох частин рівняння. Потім розділіть кожну частину рівняння на коефіцієнт (множник) при косинусі невідомого кута.
    • Наприклад, щоб ізолювати косинус невідомого кута, відніміть 164 з обох сторін рівняння, а потім розділіть кожну сторону на -160:
      144−164=164−164−160cos⁡C{\displaystyle 144-164=164-164-160\cos {C}}


  8. Обчисліть арккосинус. Так ви знайдете значення невідомого кута.[9] на калькуляторі функція арккосинуса позначається COS−1{\displaystyle COS^{-1}}.
    • Наприклад, арккосинус 0,0125 дорівнює 82,8192. Отже, кут s дорівнює 82,8192°.

Метод3 З 3:
Приклади завдань

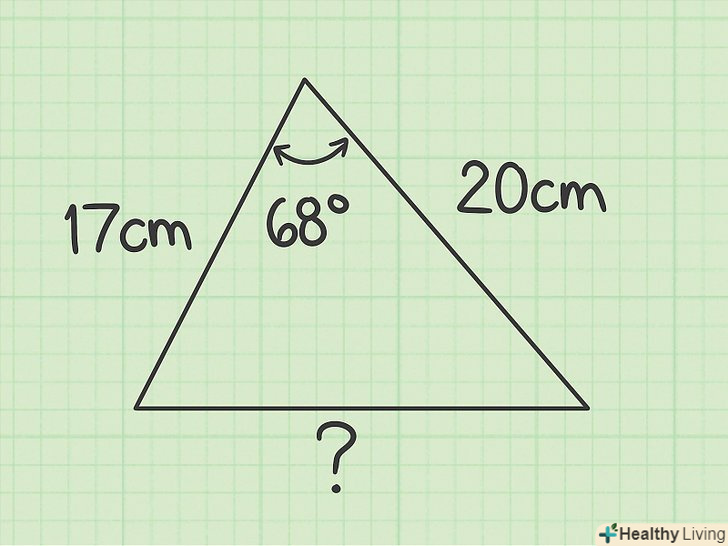
  1. Знайдіть невідому сторону трикутника.відомі сторони дорівнюють 20 см і 17 см, а кут між ними дорівнює 68°.
    • Так як дані дві сторони і кут між ними, можна використовувати теорему косинусів. Запишіть формулу:C2=a2+b2−2abcos⁡C{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos {C}}.
    • Невідома сторона — це. Підставте відомі значення у формулу: C2=202+172−2(20)(17)cos⁡68{\displaystyle c^{2}=20^{2}+17^{2}-2(20)(17)\cos {68}}.
    • ОбчислітьC2{\displaystyle c^{2}}, дотримуючись порядку математичних операцій:
      C2=202+172−2(20)(17)cos⁡68{\displaystyle c^{2}=20^{2}+17^{2}-2(20)(17)\cos {68}}

Ще почитати: