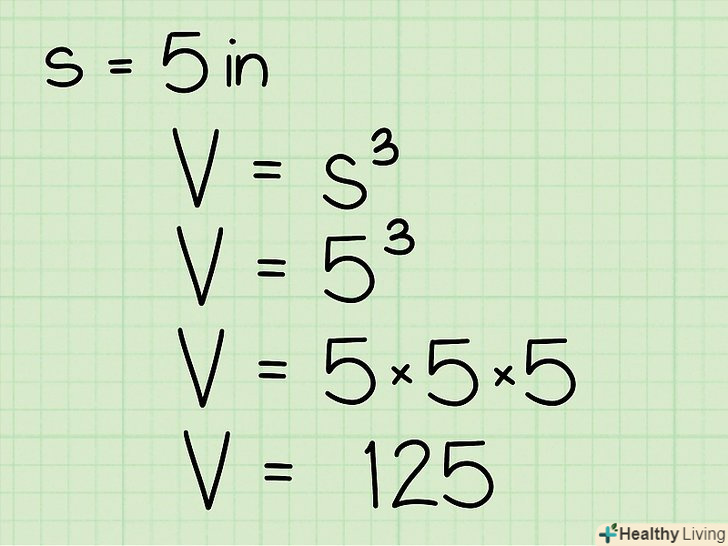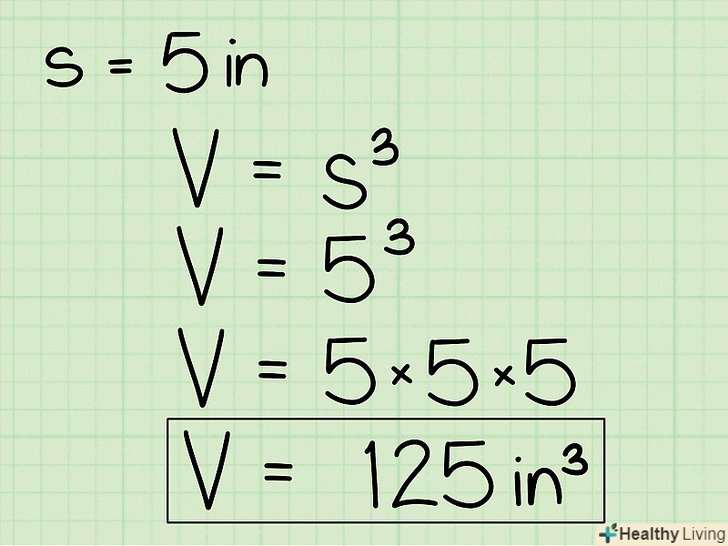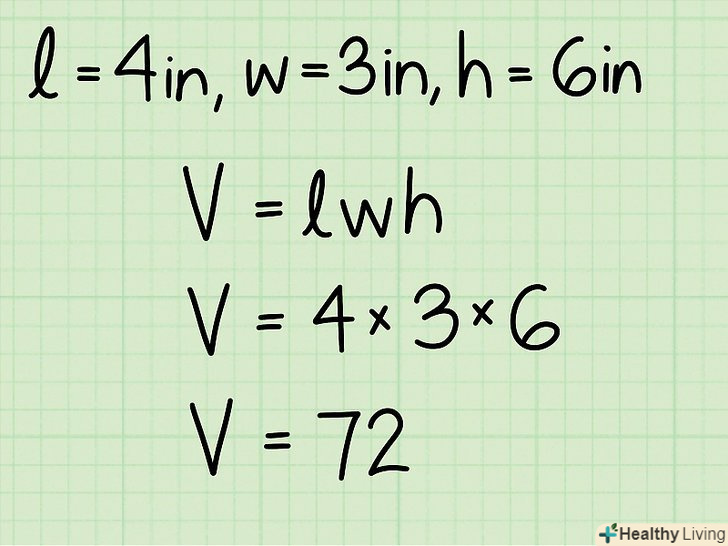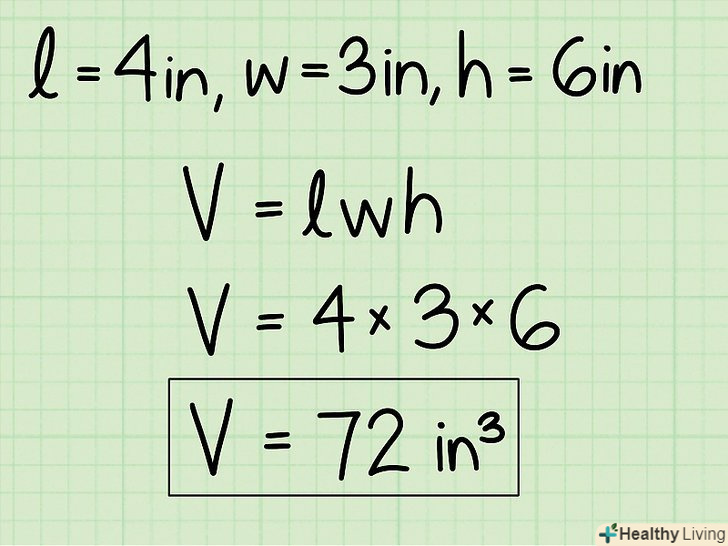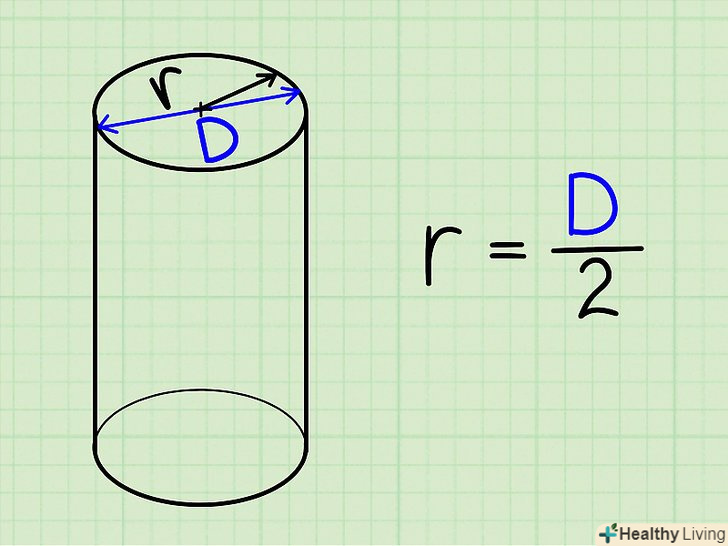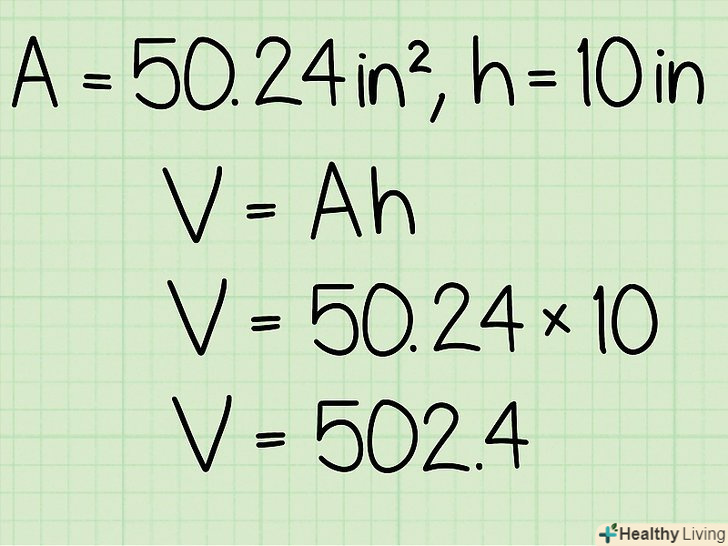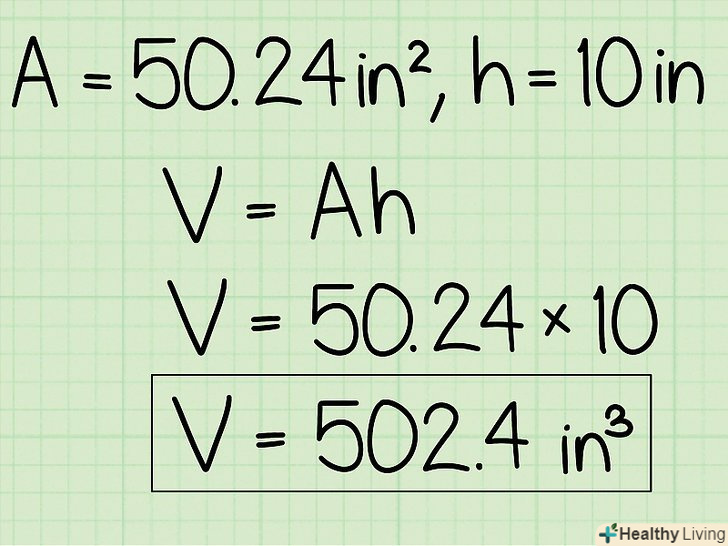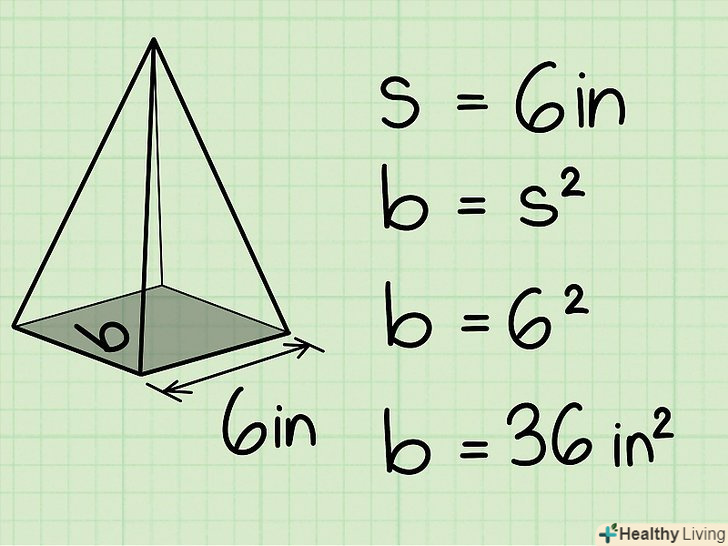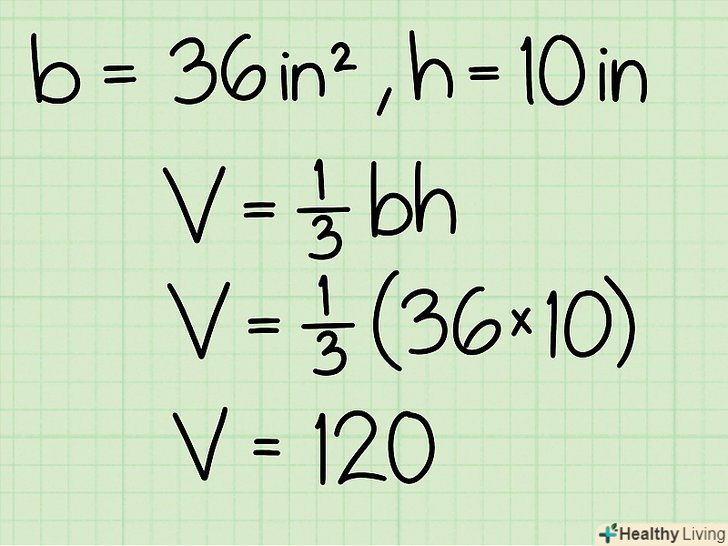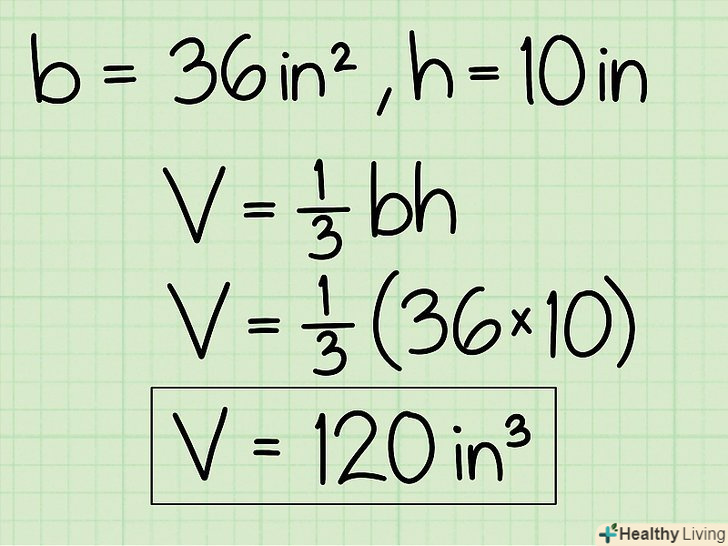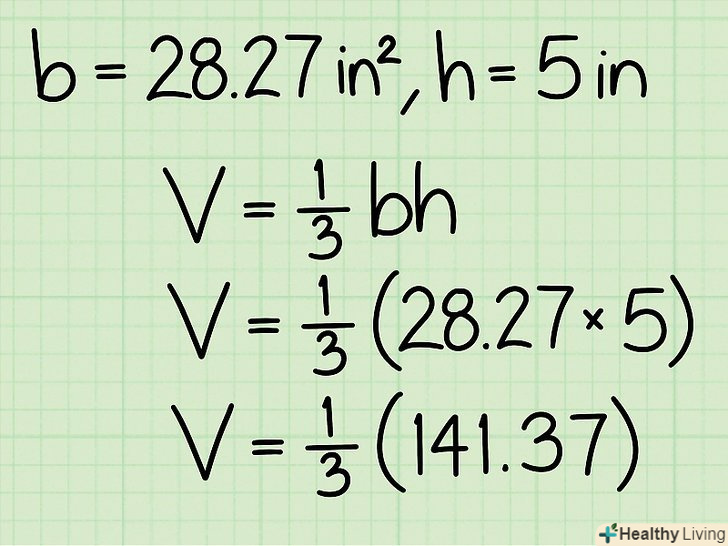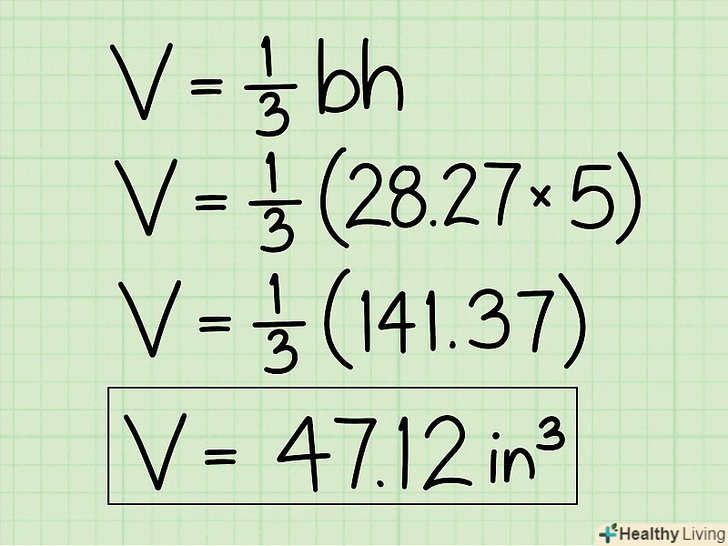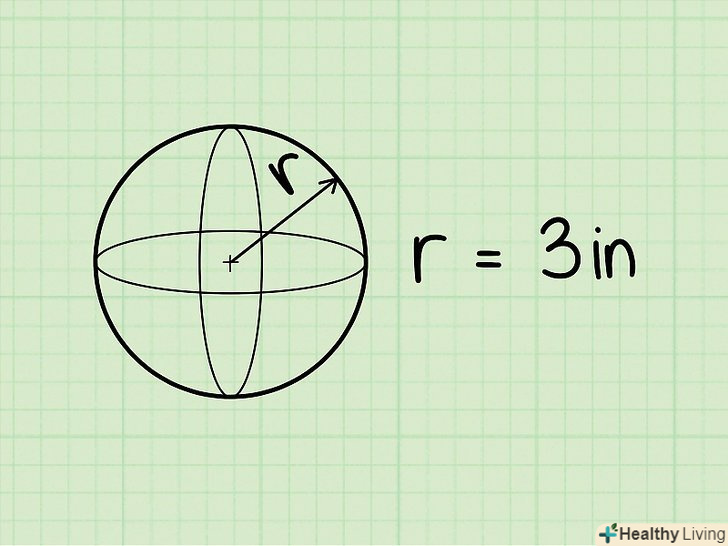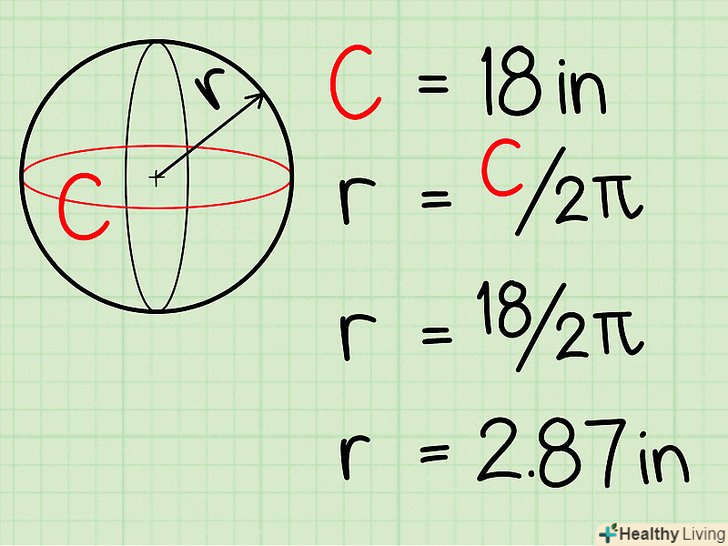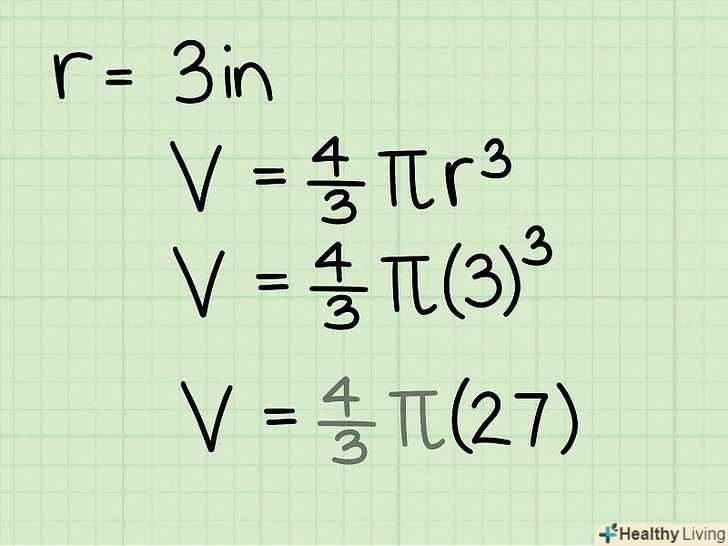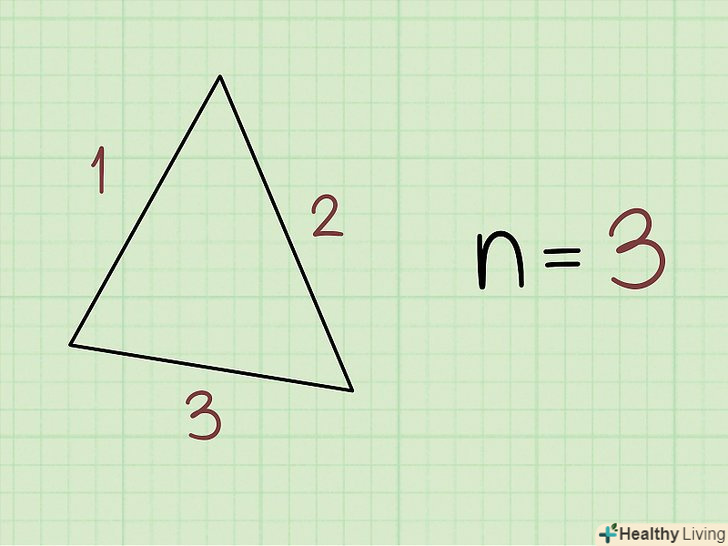Обсяг фігури являє собою займане цією фігурою тривимірний простір.[1] Уявіть собі обсяг як кількість рідини (або повітря, або піску), яким можна заповнити дану фігуру. Об'єм вимірюється в кубічних одиницях (мм3, см3, м3).[2] ця стаття розповість вам, як обчислювати обсяг шести тривимірних фігур. Ви можете помітити, що багато формули для обчислення обсягу схожі, що спрощує їх запам'ятовування.
Кроки
Метод1З 6:
Куб
Метод1З 6:
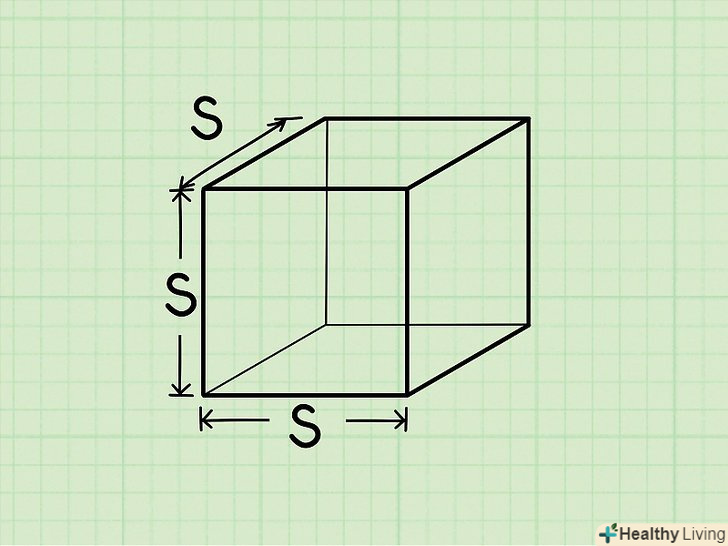
 Куб-це тривимірна фігура, яка має шість однакових квадратних граней, тобто всі її сторони (ребра) рівні. [3]
Куб-це тривимірна фігура, яка має шість однакових квадратних граней, тобто всі її сторони (ребра) рівні. [3]- Наприклад, гральна кістка-це куб.
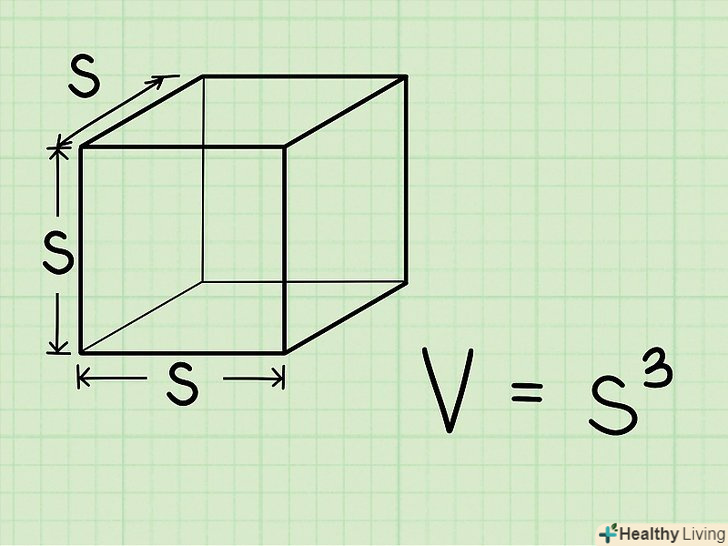
 Формула знаходження об'єму куба: V = s3, де V - об'єм, а s - довжина ребра.
Формула знаходження об'єму куба: V = s3, де V - об'єм, а s - довжина ребра.- Зведення в куб аналогічно наступному множенню: s3 = s * s * S
 Знайдіть довжину сторони (ребра) куба. вона буде дана в задачі або вам потрібно виміряти її (лінійкою або рулеткою). Оскільки ребра куба рівні, вимірюйте будь-яке ребро.
Знайдіть довжину сторони (ребра) куба. вона буде дана в задачі або вам потрібно виміряти її (лінійкою або рулеткою). Оскільки ребра куба рівні, вимірюйте будь-яке ребро.- Якщо ви не впевнені, що ваша фігура є кубом, виміряйте кожну сторону, щоб переконатися, що вони рівні. Якщо вони не рівні, перейдіть до наступного розділу.
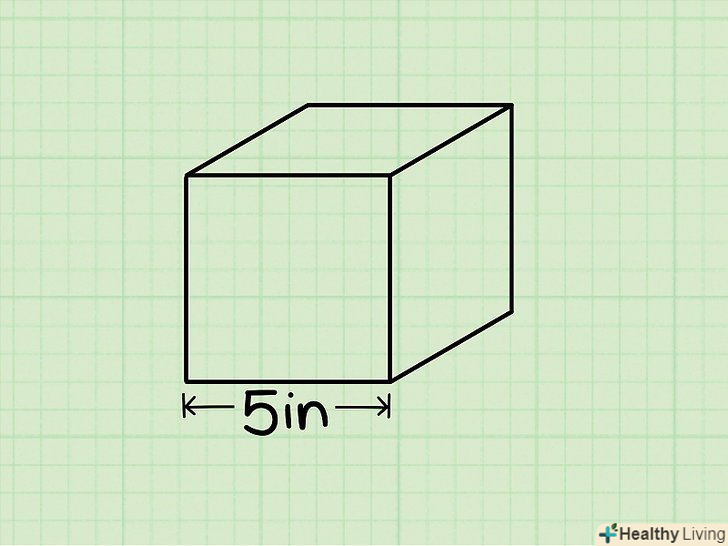
 Підставте довжину ребра куба в формулу V = s3 .наприклад, якщо ребро куба дорівнює 5 см, напишіть формулу наступним чином: V = 53 = 5 * 5 * 5 = 125 см3 – це обсяг куба.
Підставте довжину ребра куба в формулу V = s3 .наприклад, якщо ребро куба дорівнює 5 см, напишіть формулу наступним чином: V = 53 = 5 * 5 * 5 = 125 см3 – це обсяг куба. До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі ребро куба вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах. Якщо, наприклад, сторона куба дорівнює 3 см, то V = 33 = 27см3.
До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі ребро куба вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах. Якщо, наприклад, сторона куба дорівнює 3 см, то V = 33 = 27см3.
Метод2З 6:
Прямокутна призма / прямокутний паралелепіпед
Метод2З 6:
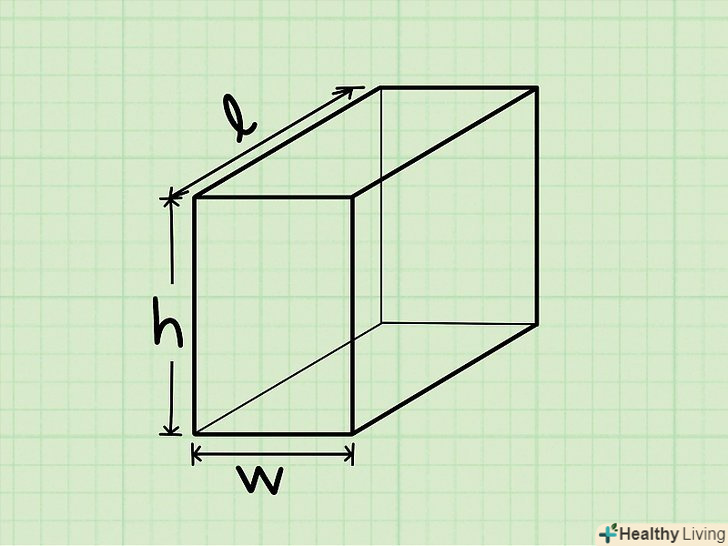
 Прямокутний паралелепіпед або прямокутна призма – це тривимірна фігура з шістьма гранями, кожна з яких є прямокутником (згадайте коробку з під взуття). [4]
Прямокутний паралелепіпед або прямокутна призма – це тривимірна фігура з шістьма гранями, кожна з яких є прямокутником (згадайте коробку з під взуття). [4]- Куб-це окремий випадок прямокутного паралелепіпеда, у якого всі ребра рівні.
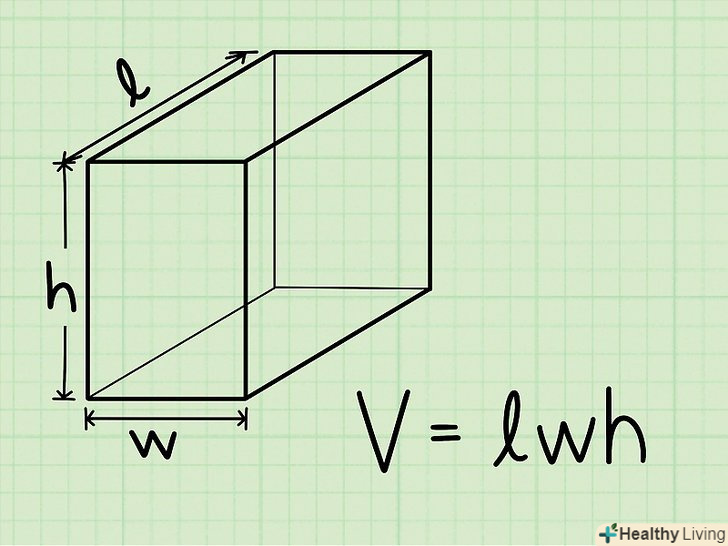
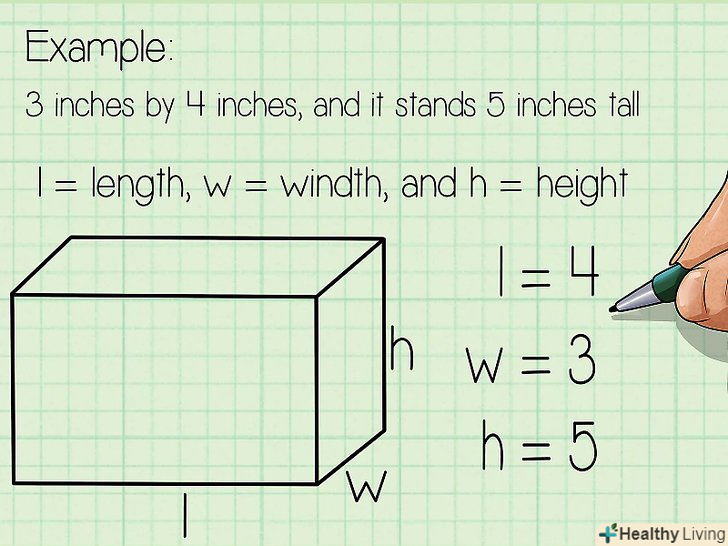
 Формула знаходження об'єму прямокутного паралелепіпеда або прямокутної призми:V = L*w*H, де V = об'єм, l = довжина, w = ширина, h = висота.[5]
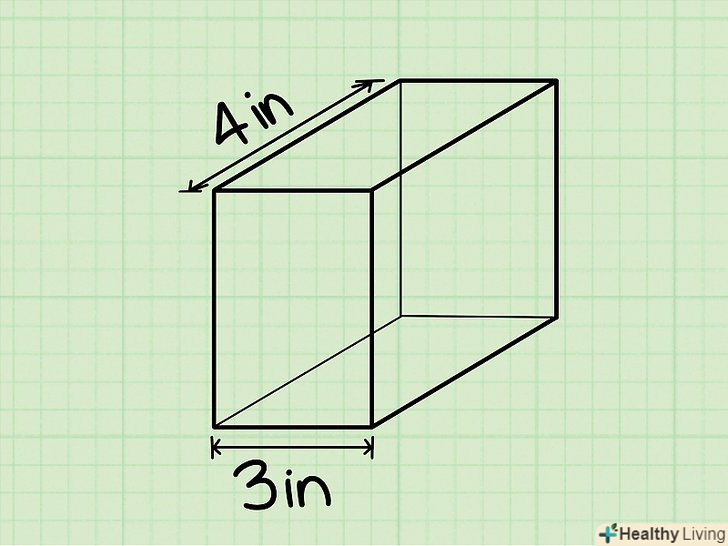
Формула знаходження об'єму прямокутного паралелепіпеда або прямокутної призми:V = L*w*H, де V = об'єм, l = довжина, w = ширина, h = висота.[5] Довжина прямокутного паралелепіпеда-це найдовше ребро верхньої або нижньої грані, тобто грані, на якій стоїть паралелепіпед (нижня грань) або паралельної їй грані (верхня грань). довжина буде дана в задачі або вам потрібно виміряти її (лінійкою або рулеткою).
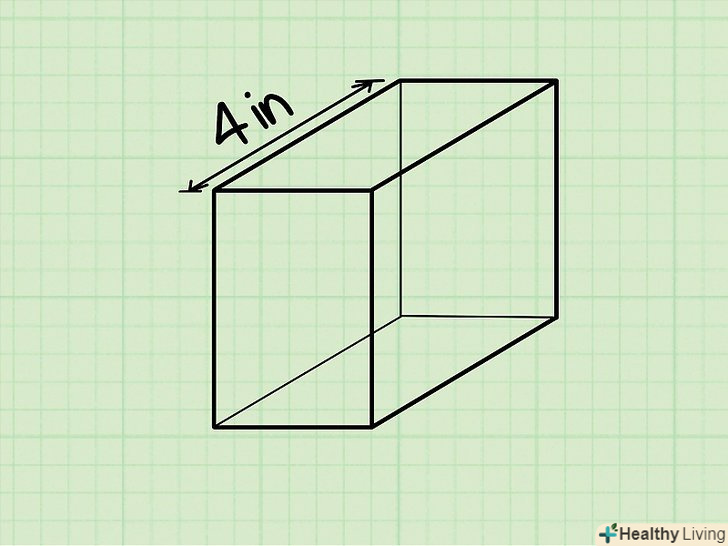
Довжина прямокутного паралелепіпеда-це найдовше ребро верхньої або нижньої грані, тобто грані, на якій стоїть паралелепіпед (нижня грань) або паралельної їй грані (верхня грань). довжина буде дана в задачі або вам потрібно виміряти її (лінійкою або рулеткою).- Приклад: довжина прямокутного паралелепіпеда дорівнює 4 см, тобто l = 4 см.
- Не турбуйтеся про те, які ребра вибрати в якості довжини, ширини і висоти. У будь-якому випадку в результаті ви отримаєте правильну відповідь (тільки виміряйте три ребра, перпендикулярні один одному).
 Ширина прямокутного паралелепіпеда-це найкоротше ребро верхньої або нижньої грані, тобто грані, на якій стоїть паралелепіпед (нижня грань) або паралельної їй грані (верхня грань). Ширина буде дана в задачі або вам потрібно виміряти її (лінійкою або рулеткою).
Ширина прямокутного паралелепіпеда-це найкоротше ребро верхньої або нижньої грані, тобто грані, на якій стоїть паралелепіпед (нижня грань) або паралельної їй грані (верхня грань). Ширина буде дана в задачі або вам потрібно виміряти її (лінійкою або рулеткою).- Приклад: ширина прямокутного паралелепіпеда дорівнює 3 см, тобто w = 3 см.
- Якщо ви вимірюєте ребра паралелепіпеда лінійкою або рулеткою, не забудьте виміряти їх в однакових одиницях виміру. Не вимірюйте одне ребро в міліметрах, а інше в сантиметрах.
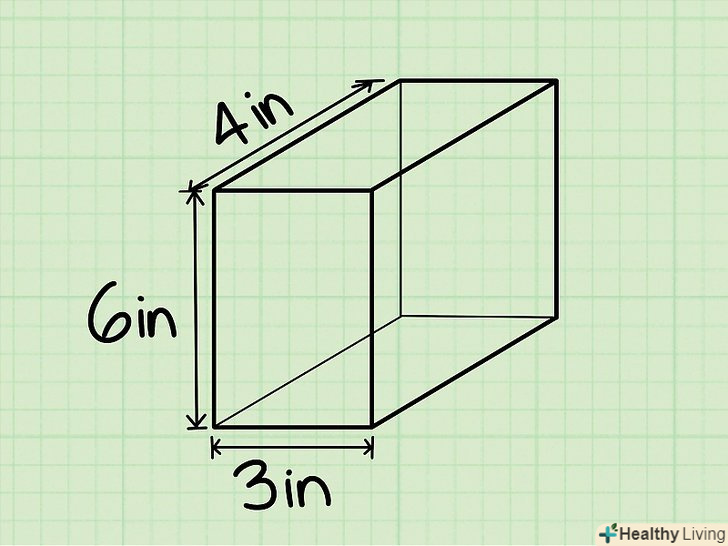
 Висота прямокутного паралелепіпеда-це відстань між його нижньою і верхньою гранями. висота буде дана в задачі або вам потрібно виміряти її (лінійкою або рулеткою).
Висота прямокутного паралелепіпеда-це відстань між його нижньою і верхньою гранями. висота буде дана в задачі або вам потрібно виміряти її (лінійкою або рулеткою).- Приклад: висота прямокутного паралелепіпеда дорівнює 6 см, тобто h = 6 см.
 Підставте знайдені значення в формулу V = l*w*h.
Підставте знайдені значення в формулу V = l*w*h.- У нашому прикладі l = 4, w = 3 і h = 6. Тому V = 4*3*6 = 72.
 До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі ребра вимірювалися в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 72 см3.
До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі ребра вимірювалися в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 72 см3.- Якщо в прямокутній призмі l = 2 см, w = 4 см, h = 8 см, то V = 2*4*8 = 64 см3
Метод3З 6:
Циліндр
Метод3З 6:
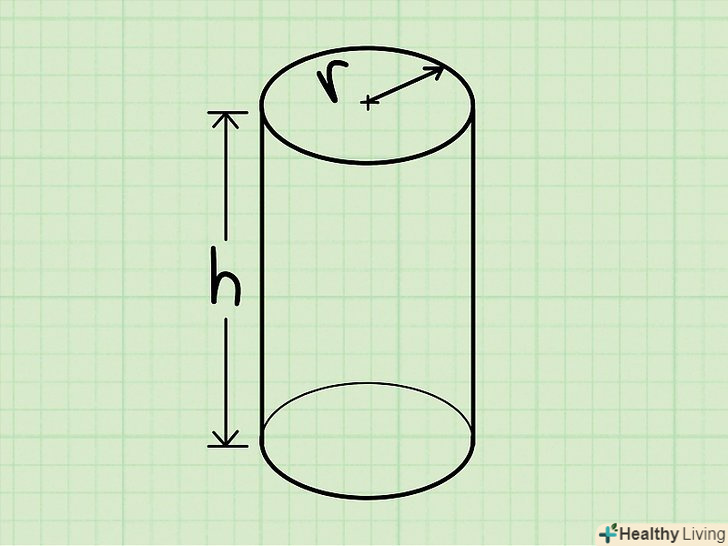
 Циліндр-це тривимірна фігура, обмежена циліндричною поверхнею і двома паралельними площинами, що перетинають її.[6]
Циліндр-це тривимірна фігура, обмежена циліндричною поверхнею і двома паралельними площинами, що перетинають її.[6]- Наприклад, банку або батарейка АА мають форму циліндра.
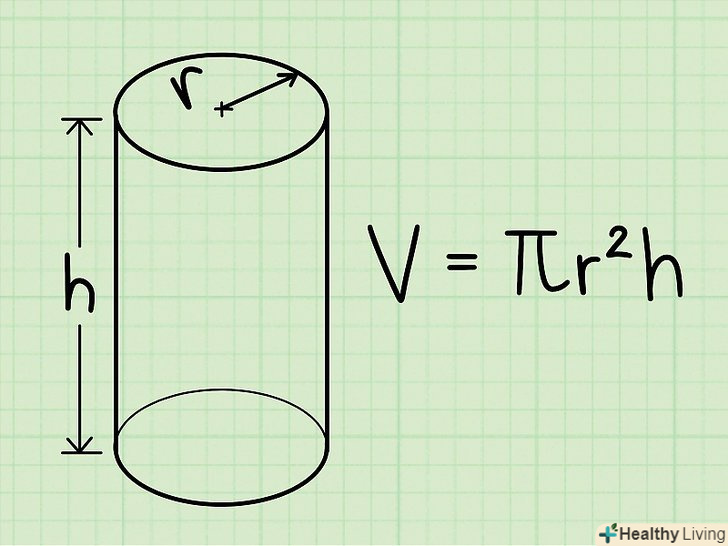
 Формула знаходження об'єму циліндра:V = πr2h, де V - об'єм, h - висота, r – радіус основи і πr2 - площа основи циліндра.
Формула знаходження об'єму циліндра:V = πr2h, де V - об'єм, h - висота, r – радіус основи і πr2 - площа основи циліндра.- У деяких завданнях відповідь потрібно представити з ПІ, а в деяких замість Пі підставити 3,14.
- Формула для знаходження об'єму циліндра насправді дуже схожа на формулу обчислення об'єму прямокутної призми, тобто ви перемножуєте висоту і площу основи. У прямокутній призмі площа основи дорівнює l * w, а в циліндрі вона дорівнює πr2.
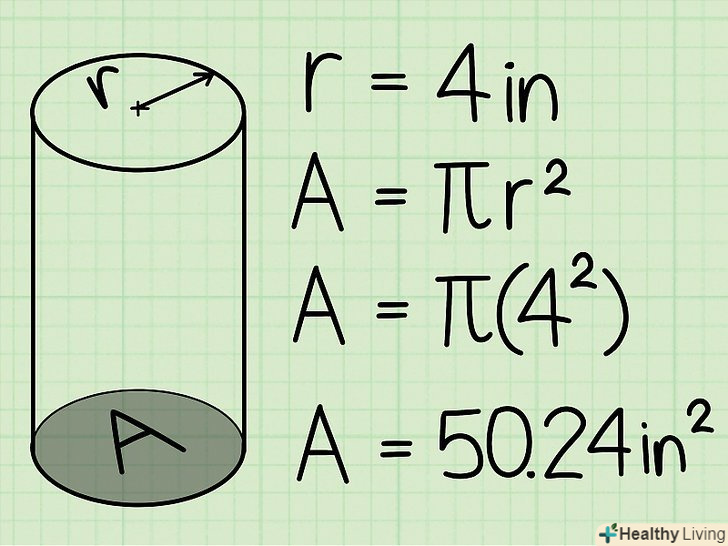
 Знайдіть радіус підстави.він, швидше за все, дано в завданні. Якщо дано діаметр, розділіть його на 2, щоб знайти радіус (d = 2r).
Знайдіть радіус підстави.він, швидше за все, дано в завданні. Якщо дано діаметр, розділіть його на 2, щоб знайти радіус (d = 2r). Якщо радіус не дано, виміряйте його.для цього виміряйте підставу циліндра за допомогою лінійки або рулетки. Вимірюйте основу в його найширшій частині (тобто виміряйте діаметр основи), а потім розділіть отримане значення на 2, щоб знайти радіус.
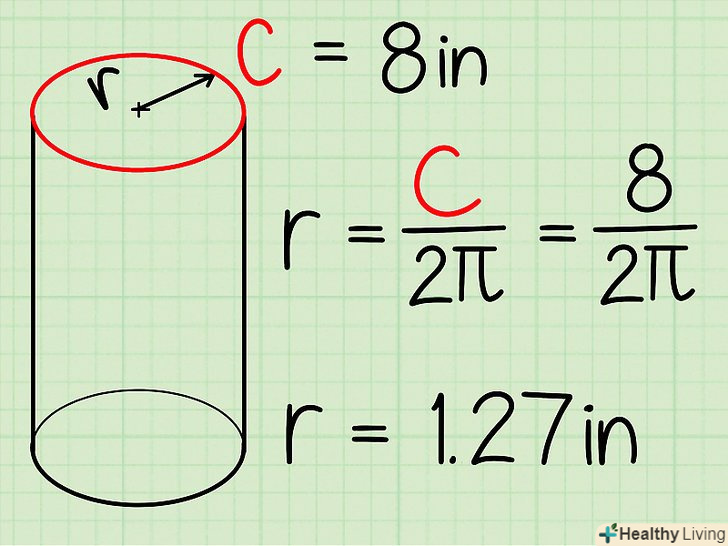
Якщо радіус не дано, виміряйте його.для цього виміряйте підставу циліндра за допомогою лінійки або рулетки. Вимірюйте основу в його найширшій частині (тобто виміряйте діаметр основи), а потім розділіть отримане значення на 2, щоб знайти радіус.- Інший варіант-виміряйте довжину кола циліндра (тобто виміряйте обхват циліндра) за допомогою рулетки, а потім знайдіть радіус за формулою r = с/2π, де с – обхват (довжина кола) циліндра (2π = 6,28).
- Наприклад, якщо обхват циліндра дорівнює 8 см, то радіус буде дорівнює 1,27 см.
- Якщо вам потрібно точне вимірювання, ви можете використовувати обидва методи, щоб переконатися, що значення радіуса збігаються (знаходження радіуса через довжину кола є більш точним методом).
 Обчисліть площу круглого підстави.для цього підставте радіус в формулу πr2.
Обчисліть площу круглого підстави.для цього підставте радіус в формулу πr2.- Якщо радіус основи дорівнює 4 см, то площа основи дорівнює π42.
- 42 = 4 * 4 = 16. 16 * π = 16 * 3,14 = 50,24 см2
- Якщо дано Діаметр підстави, то пам'ятайте, що d = 2R. Вам потрібно розділити діаметр навпіл, щоб знайти радіус.
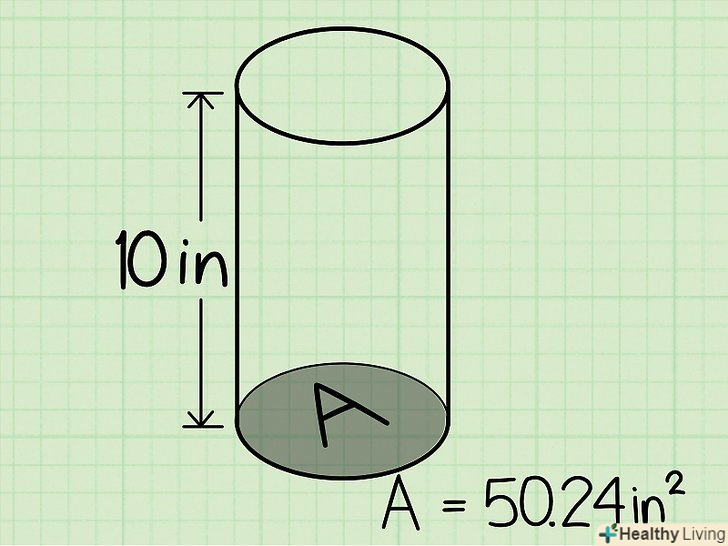
 Знайдіть висоту циліндра. Це відстань між двома круглими підставами. Висота буде дана в завданні або вам потрібно виміряти її (лінійкою або рулеткою).
Знайдіть висоту циліндра. Це відстань між двома круглими підставами. Висота буде дана в завданні або вам потрібно виміряти її (лінійкою або рулеткою). Помножте площу основи на висоту циліндра, щоб знайти його обсяг.або ж просто підставте значення відповідних величин в формулу V = πr2 h. у нашому прикладі, коли радіус підстави дорівнює 4 см, а висота дорівнює 10 см:
Помножте площу основи на висоту циліндра, щоб знайти його обсяг.або ж просто підставте значення відповідних величин в формулу V = πr2 h. у нашому прикладі, коли радіус підстави дорівнює 4 см, а висота дорівнює 10 см:- V = π4210
- Π42 = 50,24
- 50,24 * 10 = 502,4
- V = 502,4
 До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі всі величини вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 502,4 см3.
До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі всі величини вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 502,4 см3.
Метод4З 6:
Правильна піраміда
Метод4З 6:
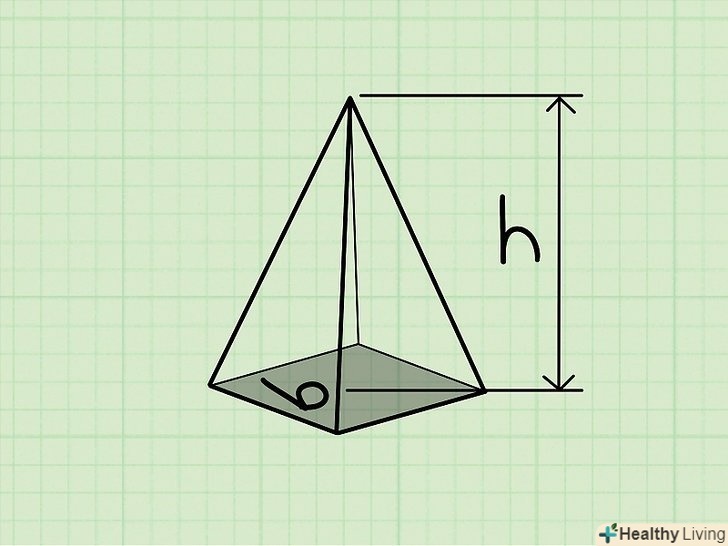
 Піраміда-це тривимірна фігура, в основі якої лежить багатокутник, а грані є трикутниками, що мають загальну вершину. [7] правильна піраміда-це тривимірна фігура, в основі якої лежить правильний багатокутник (з рівними сторонами), а вершина проектується в центр підстави.[8]
Піраміда-це тривимірна фігура, в основі якої лежить багатокутник, а грані є трикутниками, що мають загальну вершину. [7] правильна піраміда-це тривимірна фігура, в основі якої лежить правильний багатокутник (з рівними сторонами), а вершина проектується в центр підстави.[8]- Зазвичай ми представляємо піраміду, що має квадратне підставу, але в основі піраміди може лежати багатокутник з 5, 6 або навіть зі 100 сторонами!
- Піраміда з круглим підставою називається конусом, який буде обговорюватися в наступному розділі.
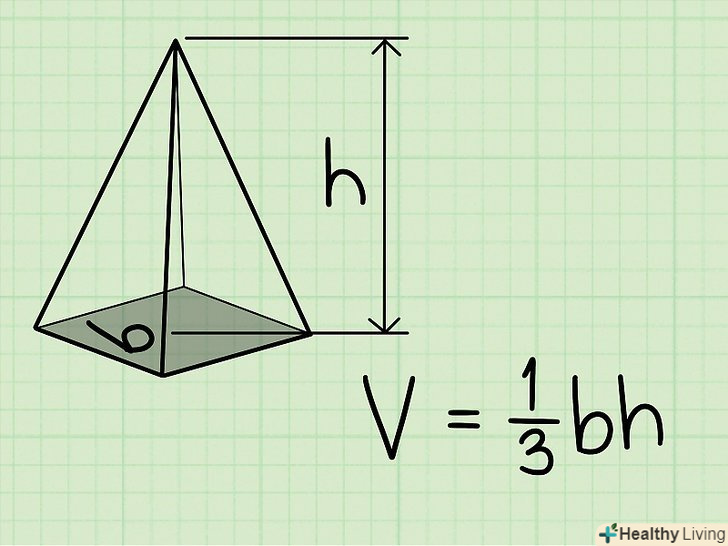
 Формула знаходження обсягу правильної піраміди: V = 1/3BH, де b – площа основи піраміди, h – висота піраміди (перпендикуляр, що з'єднує підставу і вершину піраміди).
Формула знаходження обсягу правильної піраміди: V = 1/3BH, де b – площа основи піраміди, h – висота піраміди (перпендикуляр, що з'єднує підставу і вершину піраміди).- Ця формула для обчислення обсягу піраміди однаково придатна як для правильних пірамід (в яких вершина проектується в центр підстави), так і для похилих (в яких вершина не проектується в центр підстави).
 Обчисліть площу основи.формула буде залежати від фігури, що лежить в основі піраміди. У нашому прикладі в основі піраміди лежить квадрат зі стороною 6 см.площа квадрата дорівнює s2, де s – сторона квадрата. Таким чином, в нашому прикладі площа основи піраміди дорівнює 62 = 36 см2
Обчисліть площу основи.формула буде залежати від фігури, що лежить в основі піраміди. У нашому прикладі в основі піраміди лежить квадрат зі стороною 6 см.площа квадрата дорівнює s2, де s – сторона квадрата. Таким чином, в нашому прикладі площа основи піраміди дорівнює 62 = 36 см2- Площа трикутника дорівнює 1/2BH, де h – висота трикутника, b – сторона, до якої проведена висота.
- Площа будь-якого правильного багатокутника можна обчислити за формулою: А = 1/2ра, де а – площа, р – периметр фігури, а – апофема (відрізок, що з'єднує центр фігури з серединою будь-якої сторони фігури). Для отримання додаткової інформації про знаходження площі багатокутників прочитайте цю статтю.[9]
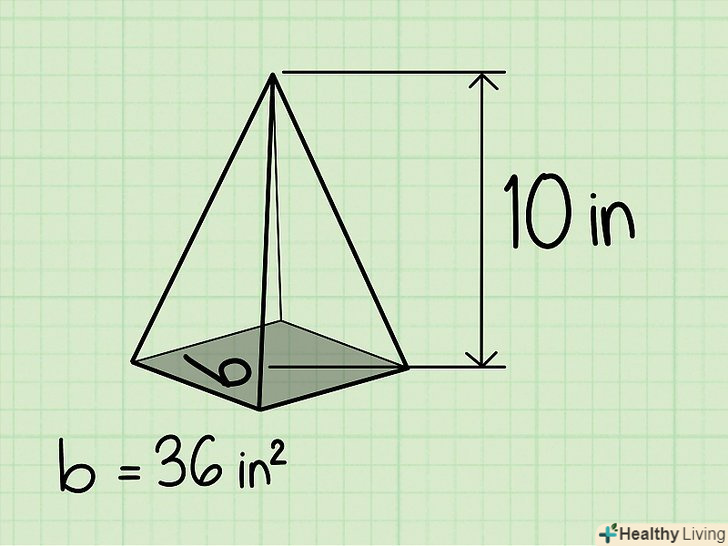
 Знайдіть висоту піраміди. висота буде дана в завданні. У нашому прикладі висота піраміди дорівнює 10 см.
Знайдіть висоту піраміди. висота буде дана в завданні. У нашому прикладі висота піраміди дорівнює 10 см. Помножте площу основи піраміди на її висоту, а потім розділіть отриманий результат на 3, щоб знайти обсяг піраміди. Формула для обчислення об'єму піраміди: V = 1/3BH. У нашому прикладі площа підстави дорівнює 36, а висота дорівнює 10, тому обсяг: 36*10*1/3 = 120.
Помножте площу основи піраміди на її висоту, а потім розділіть отриманий результат на 3, щоб знайти обсяг піраміди. Формула для обчислення об'єму піраміди: V = 1/3BH. У нашому прикладі площа підстави дорівнює 36, а висота дорівнює 10, тому обсяг: 36*10*1/3 = 120.- Якщо, наприклад, дана піраміда з п'ятикутним підставою площею 26, а висота піраміди дорівнює 8, то обсяг піраміди: 1/3*26*8 = 69,33.
 До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі всі величини вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 120 см3.
До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі всі величини вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 120 см3.
Метод5З 6:
Конус
Метод5З 6:
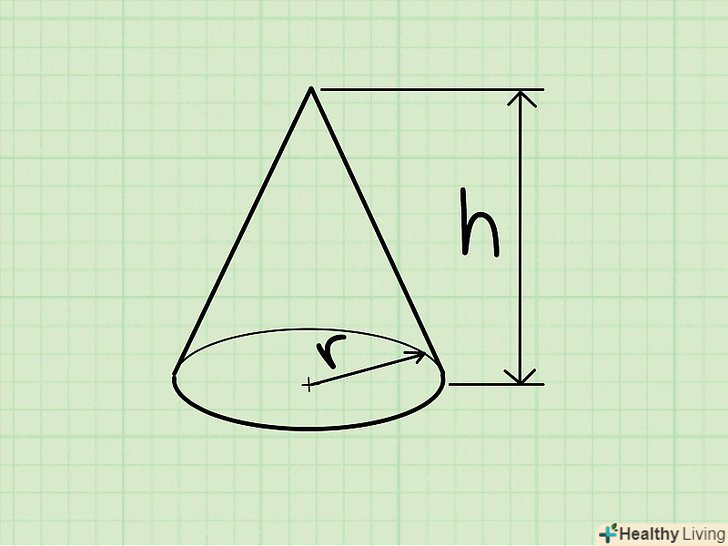
 Конус-це тривимірна фігура, яка має круглу основу і одну вершину.або конус-це особливий випадок піраміди з круглим підставою.[10]
Конус-це тривимірна фігура, яка має круглу основу і одну вершину.або конус-це особливий випадок піраміди з круглим підставою.[10]- Якщо вершина конуса знаходиться безпосередньо над центром круглого підстави, то конус називається прямим; в іншому випадку конус називається похилим. Але формула для обчислення обсягу конуса однакова для обох типів конуса.
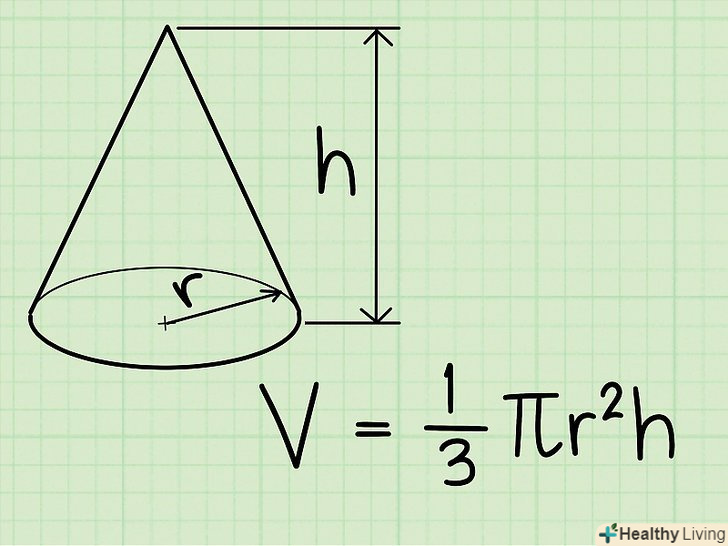
 Формула для обчислення об'єму конуса: V = 1/3πr2 h, де r – радіус круглого підстави, h – висота конуса.
Формула для обчислення об'єму конуса: V = 1/3πr2 h, де r – радіус круглого підстави, h – висота конуса.- B = πr 2 – це площа круглого підстави конуса. Таким чином, формулу для обчислення об'єму конуса можна записати так: V = 1/3BH, що збігається з формулою знаходження об'єму піраміди!
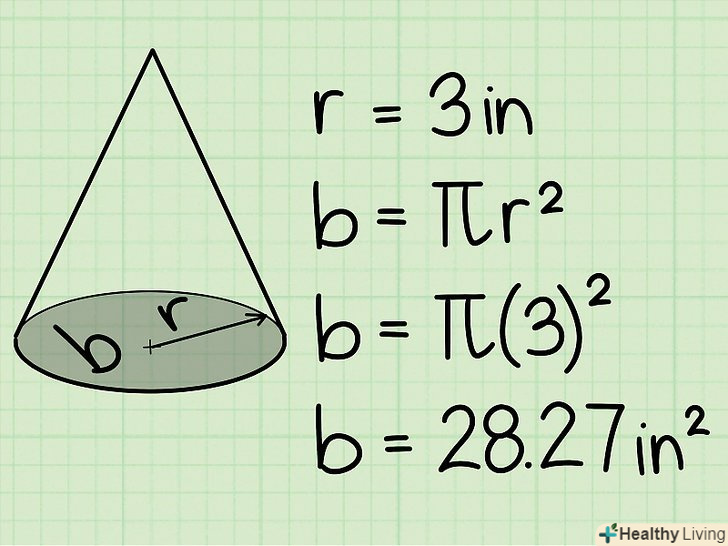
 Обчисліть площу круглого підстави.радіус повинен бути даний в задачі. Якщо дано Діаметр підстави, то пам'ятайте, що d = 2R. Вам потрібно розділити діаметр навпіл, щоб знайти радіус. Для обчислення площі круглого підстави підставте радіус в формулу πr2.
Обчисліть площу круглого підстави.радіус повинен бути даний в задачі. Якщо дано Діаметр підстави, то пам'ятайте, що d = 2R. Вам потрібно розділити діаметр навпіл, щоб знайти радіус. Для обчислення площі круглого підстави підставте радіус в формулу πr2.- Наприклад, радіус круглого підстави конуса дорівнює 3 см.тоді площа цієї основи дорівнює π32.
- Π32 = π(3*3) = 9π.
- = 28,27 см2
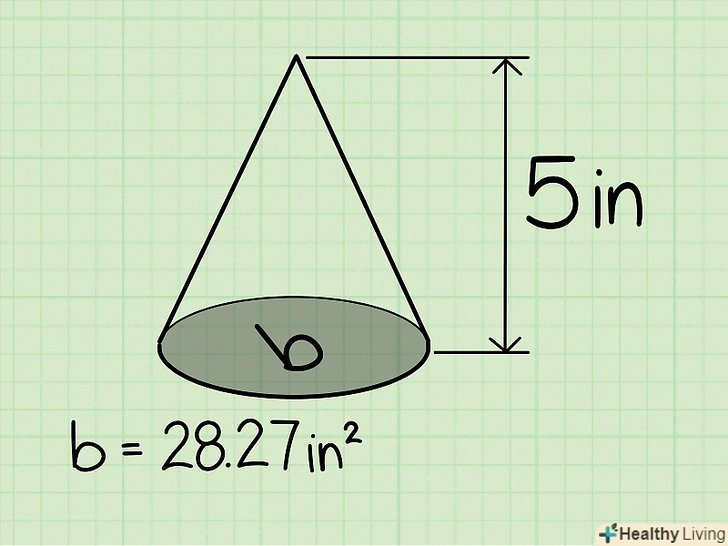
 Знайдіть висоту конуса. це перпендикуляр, опущений з вершини до основи піраміди. У нашому прикладі висота конуса дорівнює 5 см.
Знайдіть висоту конуса. це перпендикуляр, опущений з вершини до основи піраміди. У нашому прикладі висота конуса дорівнює 5 см. Перемножте висоту конуса і площу підстави.у нашому прикладі площа основи дорівнює 28,27 см2, а висота дорівнює 5 см, тому bh = 28,27 * 5 = 141,35.
Перемножте висоту конуса і площу підстави.у нашому прикладі площа основи дорівнює 28,27 см2, а висота дорівнює 5 см, тому bh = 28,27 * 5 = 141,35. Тепер помножте отриманий результат на 1/3 (або просто розділіть його на 3), щоб знайти обсяг конуса. в описаному вище кроці ви знайшли обсяг циліндра, а обсяг конуса завжди в 3 рази менше обсягу циліндра.
Тепер помножте отриманий результат на 1/3 (або просто розділіть його на 3), щоб знайти обсяг конуса. в описаному вище кроці ви знайшли обсяг циліндра, а обсяг конуса завжди в 3 рази менше обсягу циліндра.- У нашому прикладі: 141,35 * 1/3 = 47,12 – це обсяг конуса.
- Або: 1/3π325 = 47,12
 До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі всі величини вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 47,12 см3.
До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі всі величини вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 47,12 см3.
Метод6З 6:
Куля
Метод6З 6:
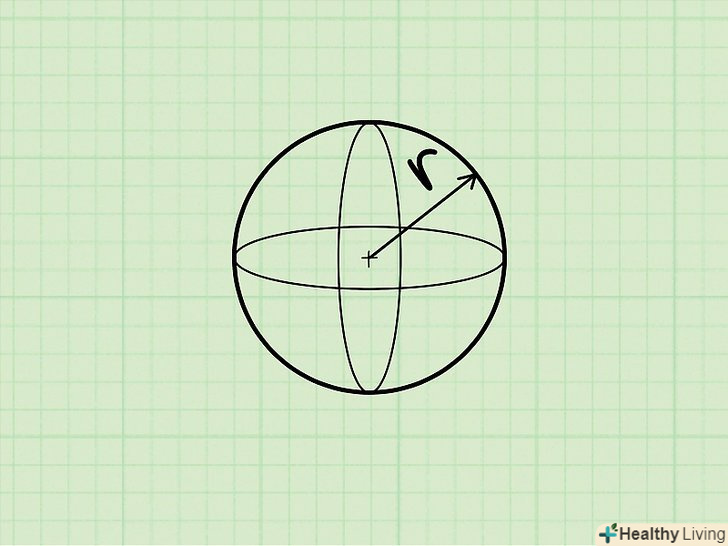
 Куля-це ідеально кругла тривимірна фігура, кожна точка поверхні якої рівновіддалена від однієї точки (центру кулі). [11]
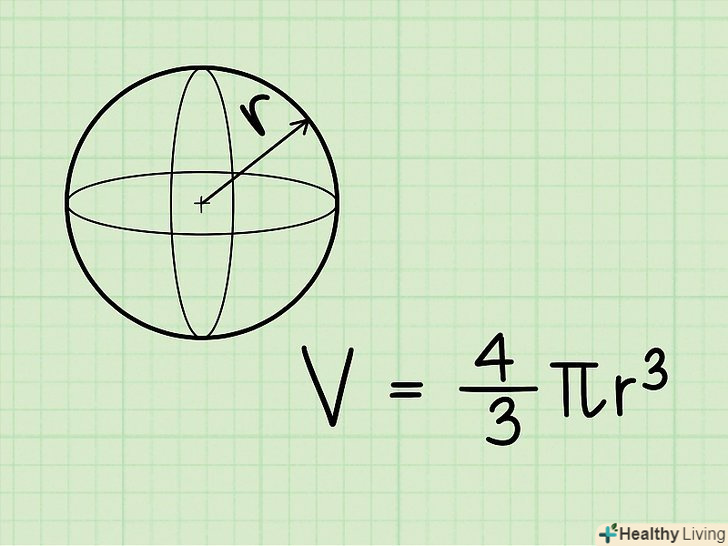
Куля-це ідеально кругла тривимірна фігура, кожна точка поверхні якої рівновіддалена від однієї точки (центру кулі). [11] Формула для обчислення об'єму кулі: V = 4/3πr3, де r – радіус кулі.[12]
Формула для обчислення об'єму кулі: V = 4/3πr3, де r – радіус кулі.[12] Знайдіть радіус кулі.радіус повинен бути даний в задачі. Якщо дано діаметр кулі, то пам'ятайте, що d = 2R. Вам потрібно розділити діаметр навпіл, щоб знайти радіус. Наприклад, радіус кулі дорівнює 3 см.
Знайдіть радіус кулі.радіус повинен бути даний в задачі. Якщо дано діаметр кулі, то пам'ятайте, що d = 2R. Вам потрібно розділити діаметр навпіл, щоб знайти радіус. Наприклад, радіус кулі дорівнює 3 см. Якщо радіус не дано, обчисліть його.для цього виміряйте довжину кола кулі (наприклад, тенісного м'яча) в його найширшій частині за допомогою мотузки, нитки або іншого подібного предмета. Потім виміряйте довжину мотузки, щоб знайти довжину кола. Розділіть отримане значення на 2π (або на 6,28), щоб обчислити радіус кулі.
Якщо радіус не дано, обчисліть його.для цього виміряйте довжину кола кулі (наприклад, тенісного м'яча) в його найширшій частині за допомогою мотузки, нитки або іншого подібного предмета. Потім виміряйте довжину мотузки, щоб знайти довжину кола. Розділіть отримане значення на 2π (або на 6,28), щоб обчислити радіус кулі.- Наприклад, якщо ви виміряли м'яч і знайшли, що довжина його кола дорівнює 18 см, Розділіть це число на 6,28 і отримаєте, що радіус м'яча дорівнює 2,87 см.
- Виконайте 3 вимірювання окружності кулі, а потім усередніть отримані значення (для цього складіть їх і суму розділіть на 3), щоб переконатися, що Ви отримали значення, близьке до істинного.
- Наприклад, в результаті трьох вимірювань довжини кола ви отримали наступні результати: 18 см, 17,75 см, 18,2 см. складіть ці значення: 18 + 17,5 + 18,2 = 53,95, а потім розділіть їх на 3: 53,95/3 = 17,98. Використовуйте це середнє значення в розрахунках обсягу кулі.
 Зведіть радіус в куб (r3). тобто r3 = r*r * r. у нашому прикладі r = 3, тому r3 = 3 * 3 * 3 = 27.
Зведіть радіус в куб (r3). тобто r3 = r*r * r. у нашому прикладі r = 3, тому r3 = 3 * 3 * 3 = 27. Тепер помножте отриманий результат на 4/3.ви можете використовувати калькулятор або виконати множення вручну, а потім спростити дріб. У нашому прикладі: 27 * 4/3 = 108/3 = 36.
Тепер помножте отриманий результат на 4/3.ви можете використовувати калькулятор або виконати множення вручну, а потім спростити дріб. У нашому прикладі: 27 * 4/3 = 108/3 = 36. Помножте отриманий результат на π (3,14), щоб знайти об'єм кулі.
Помножте отриманий результат на π (3,14), щоб знайти об'єм кулі.- У нашому прикладі: 36 * 3,14 = 113,09.
 До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі всі величини вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 113,09 см3.
До відповіді обов'язково припишіть відповідні одиниці виміру.у наведеному прикладі всі величини вимірювалася в сантиметрах, тому обсяг буде вимірюватися в кубічних сантиметрах: 113,09 см3.
Джерела
- ↑ Http://www.mathsisfun.com/definitions/volume.html
- ↑ Http://www.mathsisfun.com/measure/us-standard-volume.html
- ↑ Https://www.mathsisfun.com/definitions/cube.html
- ↑ http://www.algebralab.org/lessons/lesson.aspx?file=Geometry_3Dprisms.xml
- ↑ Http://www.studyzone.org/mtestprep/math8/g/rectvolumel.cfm
- ↑ Https://www.mathsisfun.com/definitions/cylinder.html
- ↑ Http://www.mathwords.com/p/pyramid.htm
- ↑ Http://www.mathwords.com/r/regular_pyramid.htm
- ↑ Http://www.calculatorsoup.com/calculators/geometry-plane/polygon.php