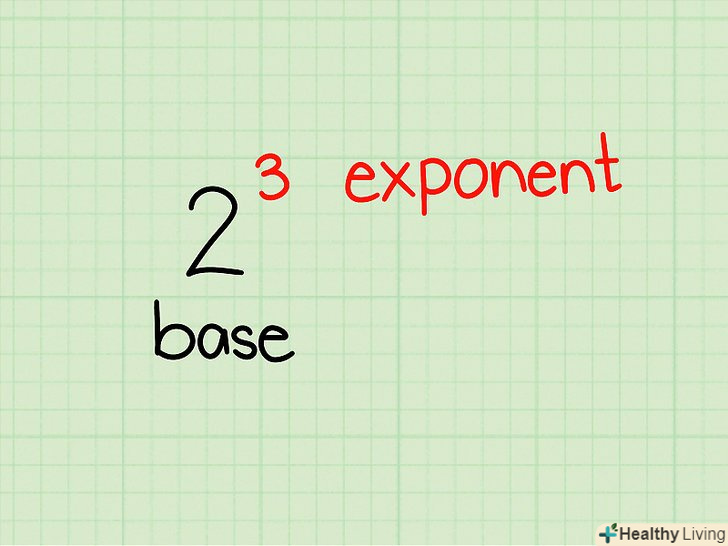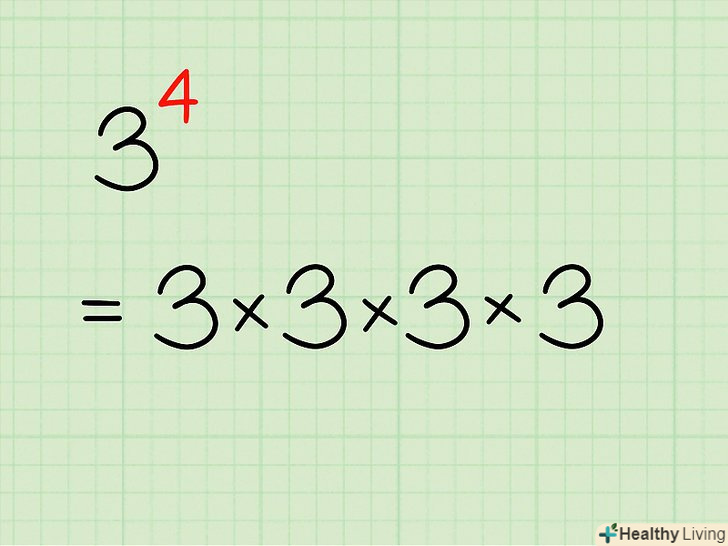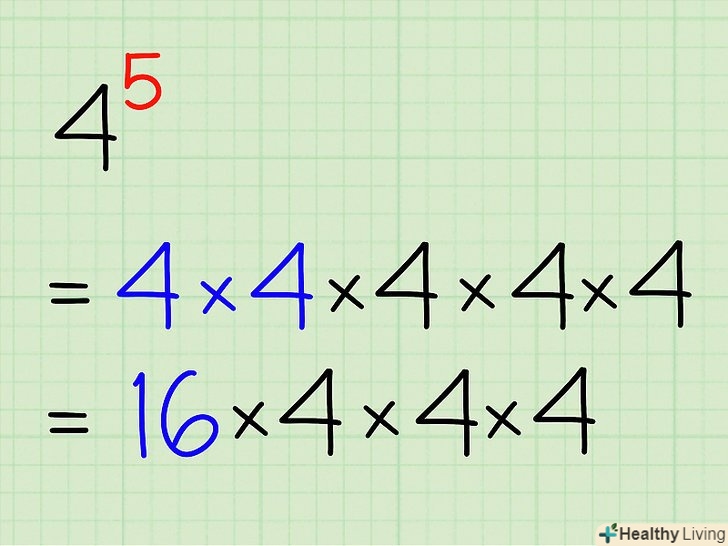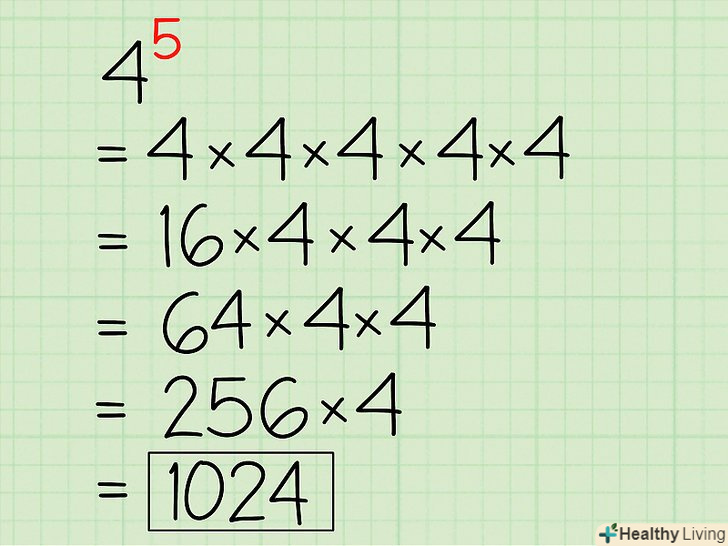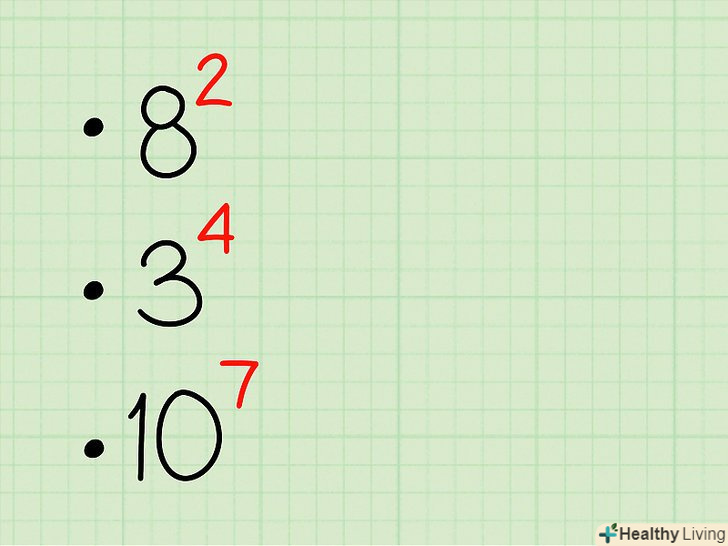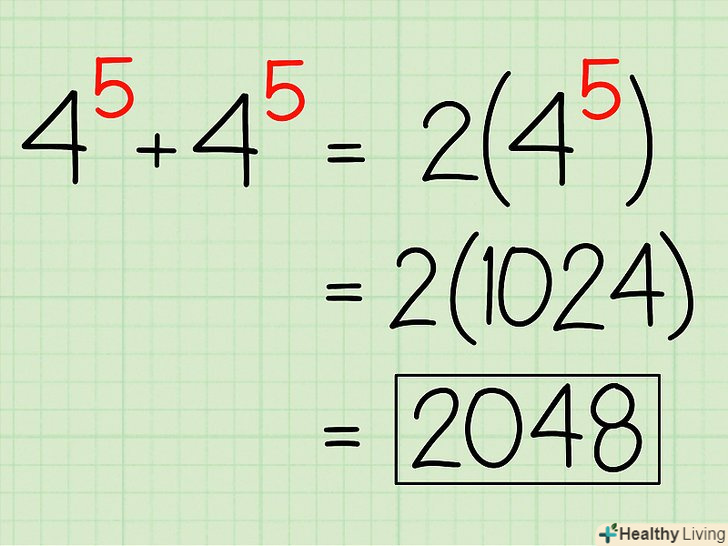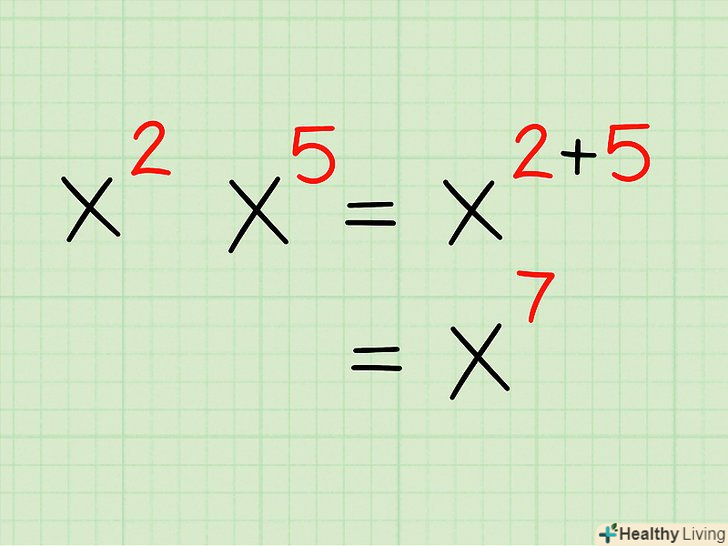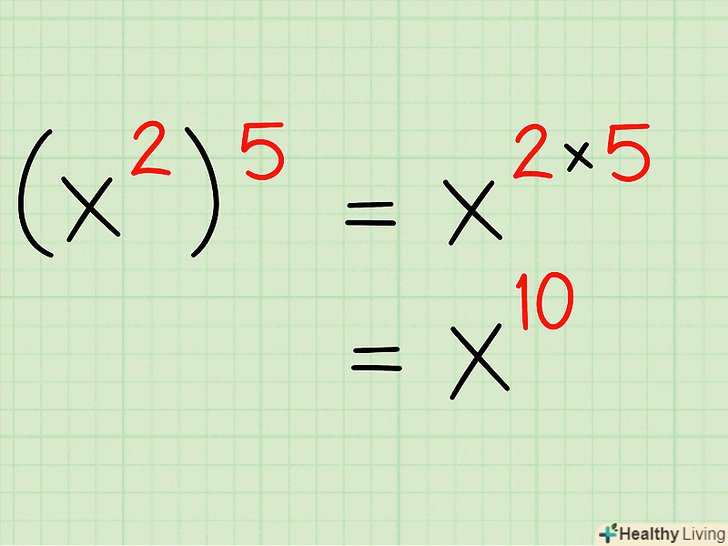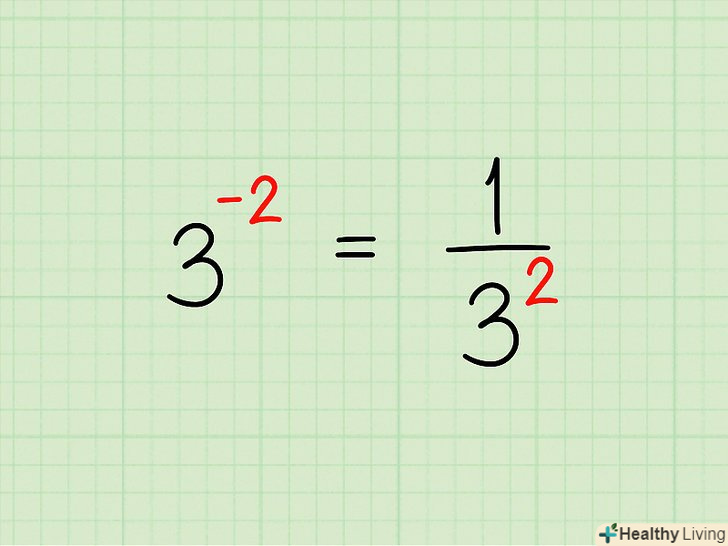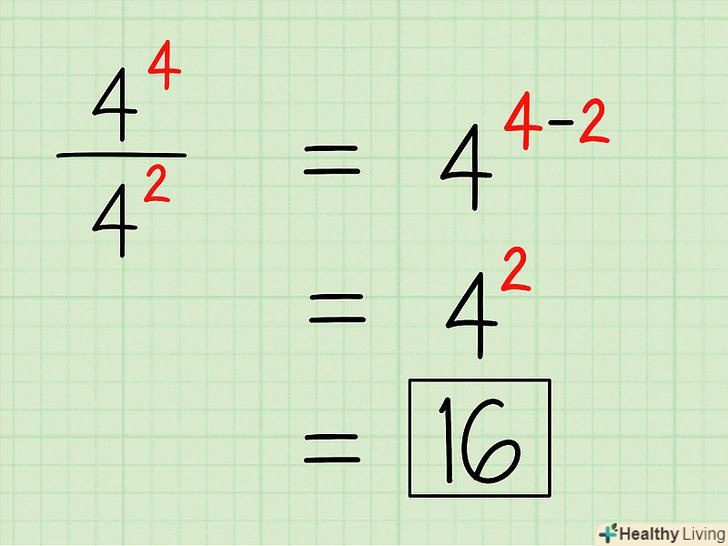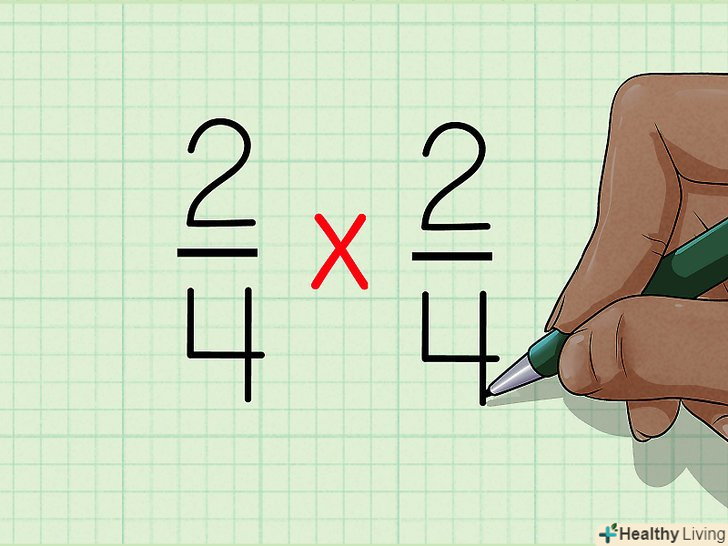Ступінь використовується для спрощення запису операції множення числа саме на себе. Наприклад, замість запису можна написати
(пояснення такого переходу дано в першому розділі цієї статті). Ступені дозволяють спростити написання довгих або складних виразів або рівнянь; також ступені легко складаються і віднімаються, що призводить до спрощення виразу або рівняння (наприклад,
).
Примітка: якщо вам необхідно вирішити показове рівняння (в такому рівнянні невідоме знаходиться в показнику ступеня), прочитайте цю статтю.
Кроки
Метод1З 3:
Розв'язування найпростіших задач зі ступенями
Метод1З 3:
 Термінологія. наприклад, дана ступінь
Термінологія. наприклад, дана ступінь. Тут 2 — цеПідстава ступеня, а 3-цеПоказник ступеня. Число
звучить так: два в третього ступеня або два в кубі.
- Якщо в показнику ступеня присутня цифра 2, наприклад,
, то такий показник називається Квадратом, тобто наш приклад озвучується так: п'ять в квадраті.
- Якщо в показнику ступеня присутня цифра 3, наприклад,
, то такий показник називається Кубом, тобто наш приклад озвучується так: десять в кубі.
- Якщо число не має показника ступеня, то це означає, що показник ступеня дорівнює 1. Наприклад,
.
- Будь-яке число (дріб, вираз), зведене в нульову ступінь, дорівнює 1, тобто
або
більш детальну інформацію ви знайдете в розділі «Поради».
- Якщо в показнику ступеня присутня цифра 2, наприклад,
 Помножте основу ступеня саме на себе числом разів, рівним показнику ступеня. якщо вам потрібно вирішити задачу зі ступенями вручну, перепишіть ступінь у вигляді операції множення, де підстава ступеня множиться саме на себе. Наприклад, дана ступінь
Помножте основу ступеня саме на себе числом разів, рівним показнику ступеня. якщо вам потрібно вирішити задачу зі ступенями вручну, перепишіть ступінь у вигляді операції множення, де підстава ступеня множиться саме на себе. Наприклад, дана ступінь. У цьому випадку підстава ступеня 3 потрібно помножити саму на себе 4 рази:
. Ось інші приклади:
- Десять в кубі
[1]
 Для початку перемножте перші два числа. наприклад,
Для початку перемножте перші два числа. наприклад,=
. Не хвилюйтеся-процес обчислення не такий складний, яким здається на перший погляд. Спочатку перемножте перші дві четвірки, а потім замініть їх отриманим результатом. Отак:
 Помножте отриманий результат (в нашому прикладі 16) на наступне число.кожен наступний результат буде пропорційно збільшуватися. У нашому прикладі помножте 16 на 4. Отак:
Помножте отриманий результат (в нашому прикладі 16) на наступне число.кожен наступний результат буде пропорційно збільшуватися. У нашому прикладі помножте 16 на 4. Отак:- Продовжуйте множити результат перемноження перших двох чисел на наступне число до тих пір, поки не отримаєте остаточну відповідь. Для цього перемножуйте перші два числа, а потім отриманий результат множте на наступне число в послідовності. Цей метод справедливий для будь-якого ступеня. У нашому прикладі ви повинні отримати:
.
 Вирішіть наступні завдання.відповідь перевірте за допомогою калькулятора.
Вирішіть наступні завдання.відповідь перевірте за допомогою калькулятора. На калькуляторі знайдіть клавішу, позначену як "exp", або «
На калькуляторі знайдіть клавішу, позначену як "exp", або «», або «^».за допомогою цієї клавіші ви будете зводити число в ступінь. Обчислити ступінь з великим показником вручну практично неможливо (наприклад, ступінь
), але калькулятор з легкістю впорається з цим завданням. У Windows 7 стандартний калькулятор можна переключити в інженерний режим; для цього натисніть «Вид» –&#gt; «Інженерний». Для перемикання в звичайний режим натисніть "Вид « - &#gt;»звичайний".
- Перевірте отриману відповідь за допомогою Google. Скориставшись клавішею " ^ " на клавіатурі комп'ютера, введіть вираз в пошуковик, який моментально відобразить правильну відповідь (і, можливо, запропонує аналогічні вирази для вивчення).
Метод2 З 3:
Сложение, віднімання, перемноження ступенів
Метод2 З 3:
 Складати і віднімати ступеня можна тільки в тому випадку, якщо у них однакові підстави.якщо потрібно скласти ступені з однаковими підставами і показниками, то ви можете замінити операцію додавання операцією множення. Наприклад, дано вираз
Складати і віднімати ступеня можна тільки в тому випадку, якщо у них однакові підстави.якщо потрібно скласти ступені з однаковими підставами і показниками, то ви можете замінити операцію додавання операцією множення. Наприклад, дано вираз. Пам'ятайте, що ступінь
можна представити у вигляді
; таким чином,
(де 1 +1 =2). Тобто порахуйте число подібних ступенів, а потім перемножте таку ступінь і це число. У нашому прикладі зведіть 4 в п'яту ступінь, а потім отриманий результат помножте на 2. Пам'ятайте, що операцію додавання можна замінити операцією множення, наприклад,
. Ось інші приклади: [2]
 При перемноженні ступенів з однаковою основою їх показники складаються (підстава не змінюється). наприклад, дано вираз
При перемноженні ступенів з однаковою основою їх показники складаються (підстава не змінюється). наприклад, дано вираз. В цьому випадку потрібно просто скласти показники, залишивши підставу без змін. Таким чином,
. Ось наочне пояснення цього правила:
- Так як підстава множиться саме на себе, то ми можемо представити це в наступному вигляді:
[3]
 При зведенні ступеня в ступінь показники перемножуються. наприклад, дана ступінь
При зведенні ступеня в ступінь показники перемножуються. наприклад, дана ступінь. Так як показники ступеня перемножуються, то
. Сенс цього правила в тому, що ви множите ступінь
саму на себе п'ять разів. Отак:
- Так як підстава одне і те ж, показники ступеня просто складаються:
 Ступінь з негативним показником слід перетворити в дріб (у зворотний ступінь).не біда, якщо ви не знаєте, що таке зворотна ступінь. Якщо вам дана степеня з від'ємним показником, наприклад,
Ступінь з негативним показником слід перетворити в дріб (у зворотний ступінь).не біда, якщо ви не знаєте, що таке зворотна ступінь. Якщо вам дана степеня з від'ємним показником, наприклад,, запишіть цю ступінь в знаменник дробу (в чисельнику поставте 1), а показник зробіть позитивним. У нашому прикладі:
. Ось інші приклади:
 При діленні ступенів з однаковою підставою їх показники віднімаються (підстава при цьому не змінюється). операція ділення протилежна операції множення. Наприклад, дано вираз
При діленні ступенів з однаковою підставою їх показники віднімаються (підстава при цьому не змінюється). операція ділення протилежна операції множення. Наприклад, дано вираз. Відніміть показник ступеня, що стоїть в знаменнику, з показника ступеня, що стоїть в чисельнику (підстава не міняйте). Таким чином,
= 16.
- Ступінь, що стоїть в знаменнику, можна записати в такому вигляді:
=
. Пам'ятайте, що дріб-це число (ступінь, вираз) з негативним показником ступ
- Ступінь, що стоїть в знаменнику, можна записати в такому вигляді: