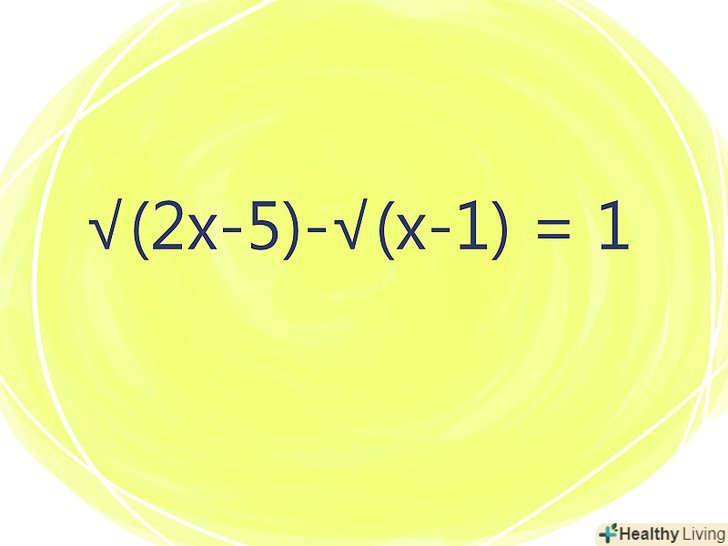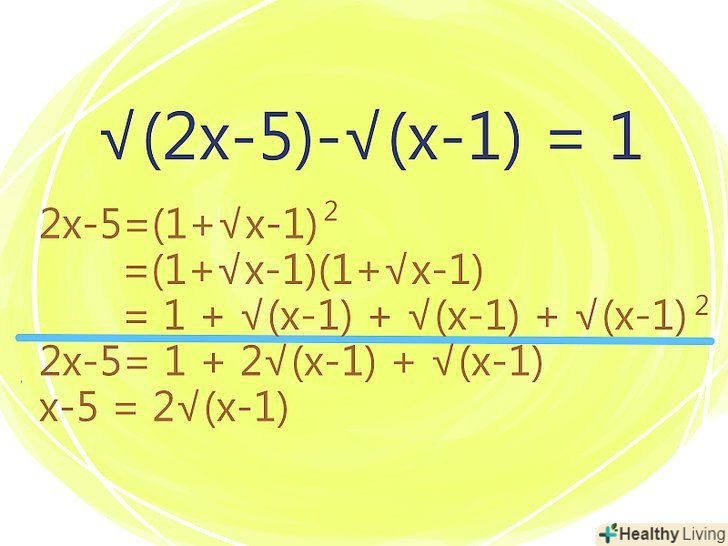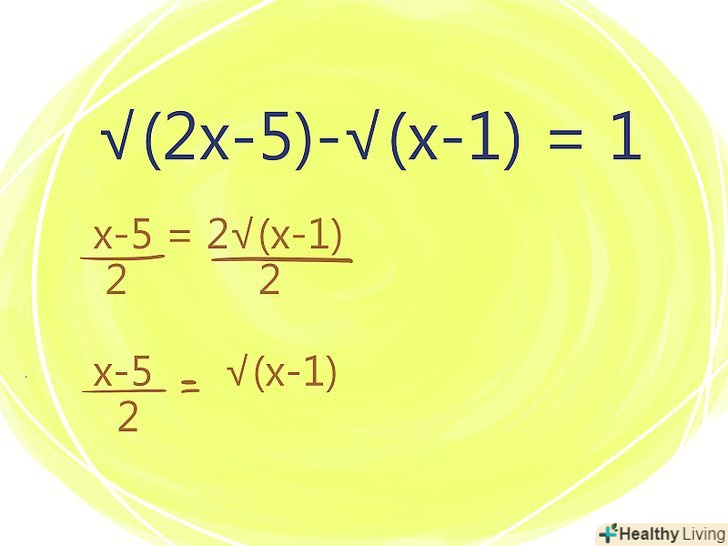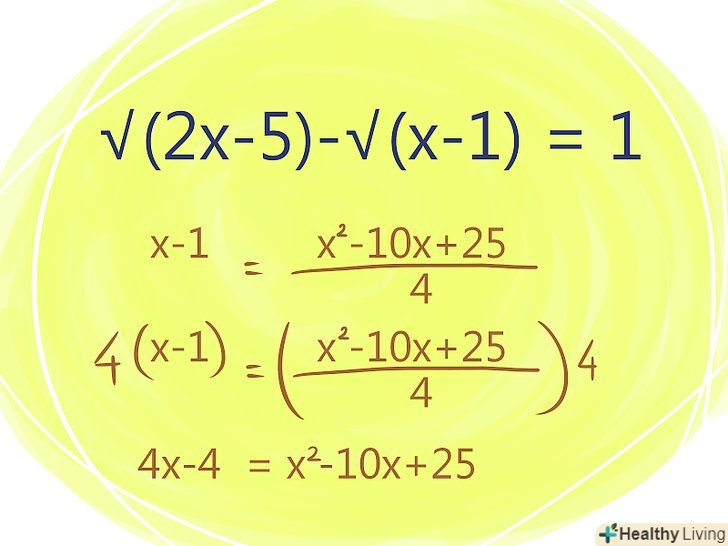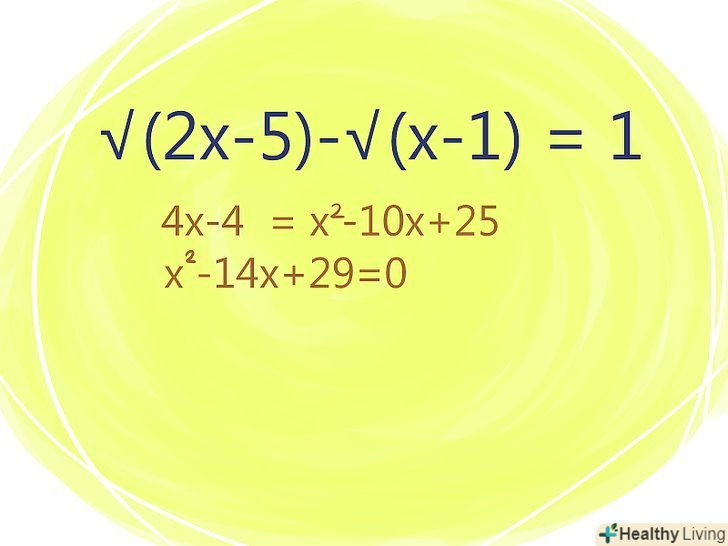Ірраціональне рівняння-це рівняння, в якому змінна знаходиться під знаком кореня. Для вирішення такого рівняння необхідно позбутися від кореня. Однак це може призвести до появи сторонніх коренів, які не є рішеннями вихідного рівняння. Для виявлення таких коренів необхідно підставити всі знайдені коріння в початкове рівняння і перевірити, чи дотримується рівність.
Кроки
Запишіть рівняння.- Рекомендується використовувати олівець, щоб мати можливість виправляти помилки.
- Розглянемо приклад: √(2x - 5)-√(х-1) = 1.
- Тут √ - це квадратний корінь.
-
Відокремте один з коренів на одній стороні рівняння.
- У нашому прикладі: √(2x-5) = 1 + √(х-1)
-
Зведіть обидві сторони рівняння в квадрат, щоб позбутися від одного кореня.
-
Спростіть рівняння, склавши / віднімаючи подібні члени.
- Повторіть описаний вище процес для позбавлення від другого кореня.
- Для цього відокремте залишився корінь на одній стороні рівняння.
- Зведіть обидві сторони рівняння в квадрат, щоб позбутися від залишився кореня.
- Для цього відокремте залишився корінь на одній стороні рівняння.
- Спростіть рівняння, склавши / віднімаючи подібні члени.
-
- Складіть / відніміть подібні члени, а потім перенесіть всі члени рівняння вліво і прирівняйте їх до нуля. Ви отримаєте квадратне рівняння.
- Вирішіть квадратне рівняння через формулу знаходження коренів квадратного рівняння.
- Рішення квадратного рівняння показано на наступному малюнку:
- Ви отримаєте: (х - 2,53) (х – 11,47) = 0.
- Таким чином, х1 = 2,53 і х2 = 11,47.
- Рішення квадратного рівняння показано на наступному малюнку:
- Підставте знайдені корені у вихідне рівняння і відкиньте сторонні корені.
- Підставте х = 2,53.
- - 1 = 1, тобто рівність не дотримано і х1 = 2,53 є стороннім коренем.
- Підставте х2 = 11,47.
- Рівність дотримана і х2 = 11,47 є рішенням рівняння.
- Таким чином, відкиньте сторонній корінь х1 = 2,53 і запишіть відповідь: x2 = 11,47.
- Підставте х = 2,53.
