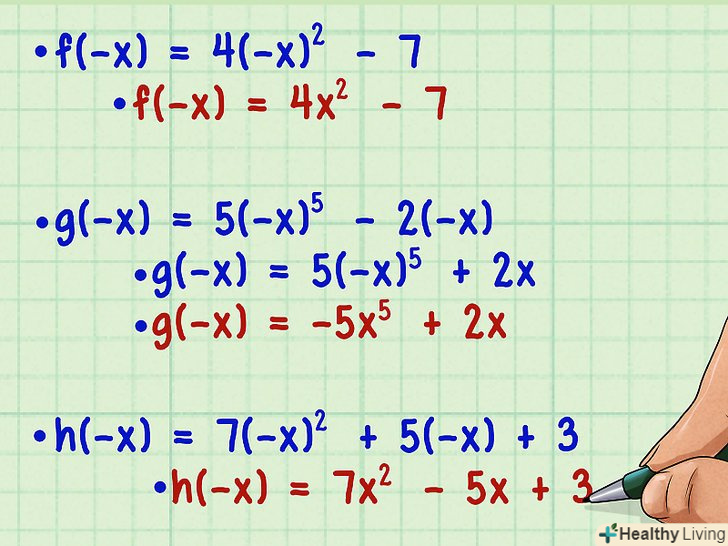Функції бувають парними, непарними або загального вигляду (тобто ні парними, ні непарними). Вид функції залежить від наявності або відсутності симетрії. Найкращий спосіб визначити вид функції-це виконати ряд алгебраїчних обчислень. Але вид функції можна з'ясувати і за її графіком. Якщо навчитися визначати вид функцій, можна передбачати поведінку певних поєднань функцій.
Кроки
Метод1 З 2:
Алгебраїчний спосіб
Метод1 З 2:
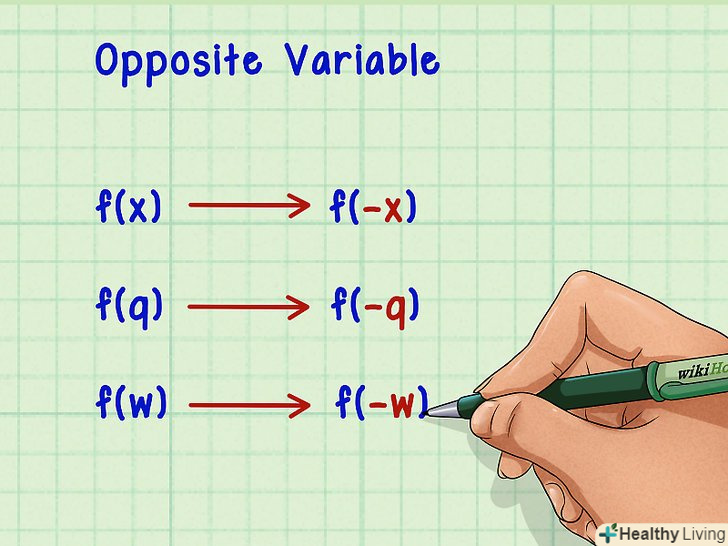
 Запам'ятайте, що таке протилежні значення змінних. в алгебрі протилежне значення змінної записується зі знаком " - " (мінус). Причому це вірно при будь-якому позначенні незалежної змінної (буквою
Запам'ятайте, що таке протилежні значення змінних. в алгебрі протилежне значення змінної записується зі знаком " - " (мінус). Причому це вірно при будь-якому позначенні незалежної змінної (буквоюабо будь-який інший літерою). Якщо у вихідній функції перед змінною вже стоїть негативний знак, то її протилежним значенням буде позитивна змінна. Нижче наведено приклади деяких змінних та їх протилежних значень:[1]
- Протилежним значенням для
є
.
- Протилежним значенням для
є
.
- Протилежним значенням для
є
.
- Протилежним значенням для
 Замініть незалежну змінну на її протилежне значення.тобто поміняйте знак незалежної змінної на протилежний. Наприклад: [2]
Замініть незалежну змінну на її протилежне значення.тобто поміняйте знак незалежної змінної на протилежний. Наприклад: [2]перетворюється в
перетворюється в
перетворюється в
.
 Спростіть нову функцію.на цьому етапі замість незалежної змінної не потрібно підставляти певні числові значення. Необхідно просто спростити нову функцію f (- x), щоб порівняти її з вихідною функцією f (x). Згадайте основне правило зведення в ступінь: при зведенні негативної змінної в парну ступінь вийде позитивна змінна, а при зведенні негативної змінної в непарну ступінь вийде негативна змінна.[3]
Спростіть нову функцію.на цьому етапі замість незалежної змінної не потрібно підставляти певні числові значення. Необхідно просто спростити нову функцію f (- x), щоб порівняти її з вихідною функцією f (x). Згадайте основне правило зведення в ступінь: при зведенні негативної змінної в парну ступінь вийде позитивна змінна, а при зведенні негативної змінної в непарну ступінь вийде негативна змінна.[3] Порівняйте дві функції.Порівняйте спрощену нову функцію f (- x) з вихідною функцією f(x). Запишіть відповідні члени обох функцій один під одним і порівняйте їх знаки.[4]
Порівняйте дві функції.Порівняйте спрощену нову функцію f (- x) з вихідною функцією f(x). Запишіть відповідні члени обох функцій один під одним і порівняйте їх знаки.[4]- Якщо знаки відповідних членів обох функцій збігаються, тобто f (x) = f (- x), вихідна функція парна. Приклад:
і
.
- Тут знаки членів збігаються, тому вихідна функція парна.
- Якщо знаки відповідних членів обох функцій протилежні один одному, тобто f (x) = -f (- x), вихідна функція парна. Приклад:
, але
.
- Зверніть увагу, що якщо помножити кожен член першої функції на -1, вийде друга функція. Таким чином, вихідна функція g (x) є непарною.
- Якщо нова функція не відповідає жодному з наведених прикладів, то вона є функцією загального вигляду (тобто ні парної, ні непарної). Наприклад:
, але
. Знаки перших членів обох функцій однакові, а знаки других членів протилежні. Тому ця функція є ні парною, ні непарною.
- Якщо знаки відповідних членів обох функцій збігаються, тобто f (x) = f (- x), вихідна функція парна. Приклад:
Метод2 З 2:
Графічний спосіб
Метод2 З 2:
 Побудуйте графік функції .для цього скористайтеся міліметровкою або графічним калькулятором. Виберіть декілька будь-яких числових значень незалежної змінної
Побудуйте графік функції .для цього скористайтеся міліметровкою або графічним калькулятором. Виберіть декілька будь-яких числових значень незалежної змінноїі підставте їх у функцію, щоб обчислити значення залежної змінної
. Знайдені координати точок нанесіть на координатну площину, а потім з'єднайте ці точки, щоб побудувати графік функції.[5]
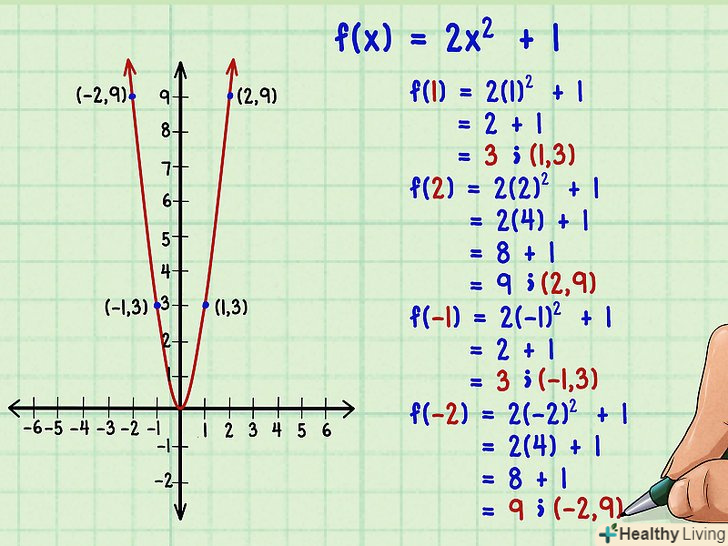
- У функцію підставте позитивні числові значення
і відповідні негативні числові значення. Наприклад, дана функція
. Підставте в неї такі значення
:
. Отримали точку з координатами
.
. Отримали точку з координатами
.
. Отримали точку з координатами
.
. Отримали точку з координатами
.
- У функцію підставте позитивні числові значення
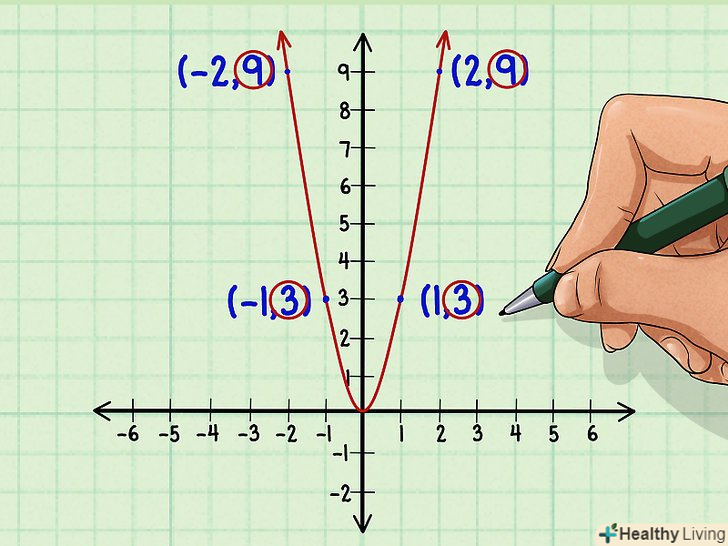
 Перевірте, чи симетричний графік функції відносно осі Y. під симетрією мається на увазі дзеркальне відображення графіка щодо осі ординат. Якщо частина графіка праворуч від осі Y (позитивні значення незалежної змінної) збігається з частиною графіка зліва від осі Y (негативні значення незалежної змінної), графік симетричний щодо осі Y. Якщо функція симетрична щодо осі ординат, така функція парна.[6]
Перевірте, чи симетричний графік функції відносно осі Y. під симетрією мається на увазі дзеркальне відображення графіка щодо осі ординат. Якщо частина графіка праворуч від осі Y (позитивні значення незалежної змінної) збігається з частиною графіка зліва від осі Y (негативні значення незалежної змінної), графік симетричний щодо осі Y. Якщо функція симетрична щодо осі ординат, така функція парна.[6]- Перевірити симетричність графіка можна по окремих точках. Якщо значення
, яке відповідає значенню
, збігається зі значенням
, яке відповідає значенню
, функція є парної. У нашому прикладі з функцією
ми отримали наступні координати точок:
- (1,3) і (-1,3)
- (2,9) і (-2,9)
- Зверніть увагу, що при x=1 І x=-1 залежна змінна у=3, а при x=2 і x=-2 залежна змінна у=9. Таким чином, функція парна. Насправді, щоб точно з'ясувати вид функції, потрібно розглянути більше двох точок, але описаний спосіб є хорошим наближенням.
- Перевірити симетричність графіка можна по окремих точках. Якщо значення
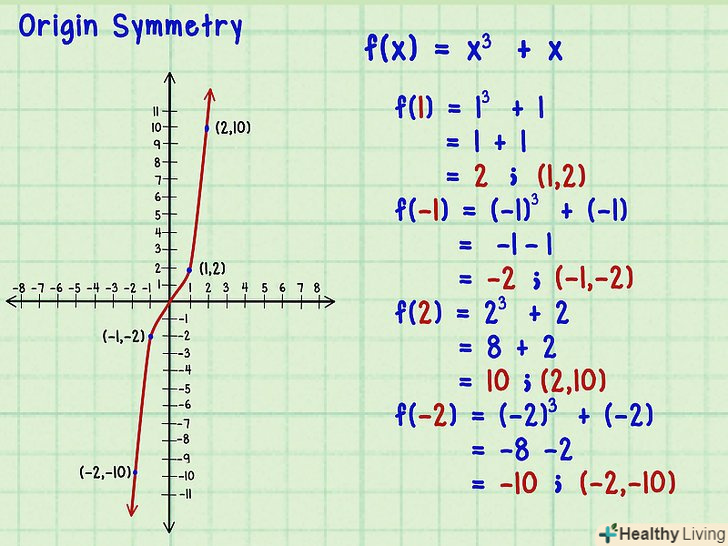
 Перевірте, чи симетричний графік функції щодо початку координат.початок координат-це точка з координатами (0,0). Симетрія щодо початку координат означає, що додатному значенню
Перевірте, чи симетричний графік функції щодо початку координат.початок координат-це точка з координатами (0,0). Симетрія щодо початку координат означає, що додатному значенню(при позитивному значенні
) відповідає від'ємне значення
(при негативному значенні
), і навпаки. Непарні функції мають симетрію щодо початку координат.[7]
- Якщо в функцію підставити кілька позитивних і відповідних негативних значень
значення
будуть відрізнятися по знаку. Наприклад, дана функція
. Підставте в неї кілька значень
:
. Отримали точку з координатами (1,2).
. Отримали точку з координатами (-1,-2).
. Отримали точку з координатами (2,10).
. Отримали точку з координатами (-2,-10).
- Таким чином, f (x) = -f (- x), тобто функція непарна.
- Якщо в функцію підставити кілька позитивних і відповідних негативних значень
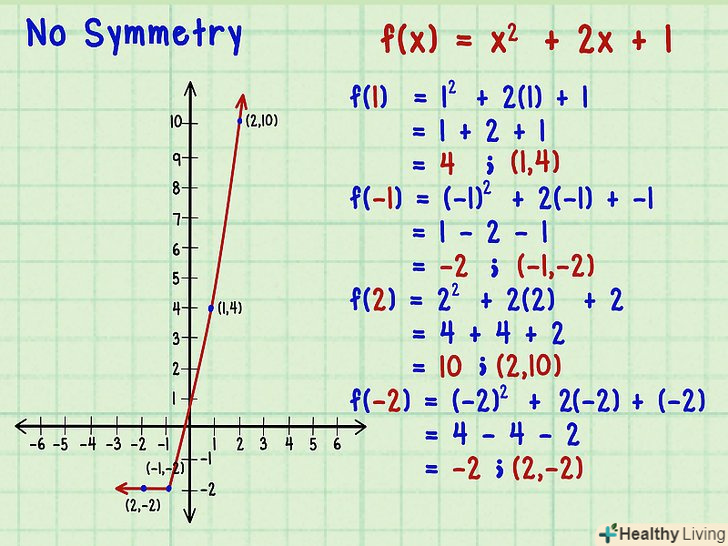
 Перевірте, чи має графік функції якусь симетрію.останній вид функції-це функція, графік якої не має симетрії, тобто дзеркальне відображення відсутнє як щодо осі ординат, так і щодо початку координат. Наприклад, дана функція
Перевірте, чи має графік функції якусь симетрію.останній вид функції-це функція, графік якої не має симетрії, тобто дзеркальне відображення відсутнє як щодо осі ординат, так і щодо початку координат. Наприклад, дана функція.[8]
- У функцію підставте кілька позитивних і відповідних негативних значень
:
. Отримали точку з координатами (1,4).
. Отримали точку з координатами (-1,-2).
. Отримали точку з координатами (2,10).
. Отримали точку з координатами (2, -2).
- Згідно з отриманими результатами, симетрії немає. Значення
для протилежних значень
не збігаються і не є протилежними. Таким чином, функція є ні парною, ні непарною.
- Зверніть увагу, що функцію
- У функцію підставте кілька позитивних і відповідних негативних значень