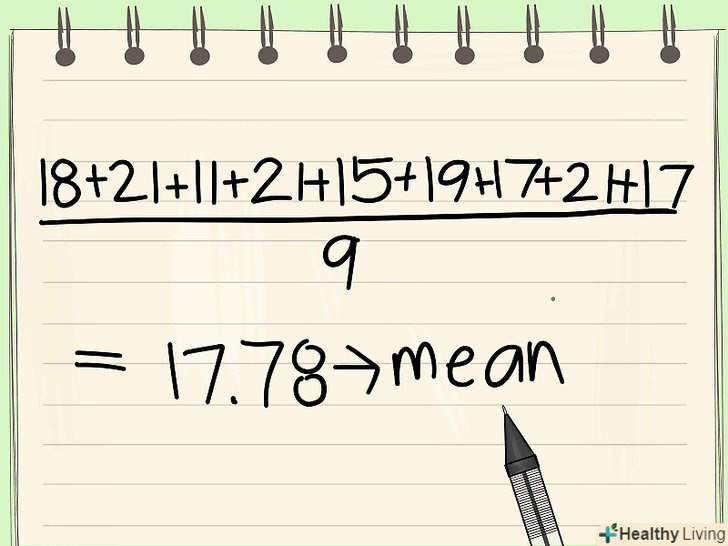Як знайти моду в безлічі чисел: 8 кроків

В статистицімодою в безлічі чисел називаєтьсяЧисло, яке зустрічається в цій множині найбільш часто. Мод може бути кілька: Якщо в наборі даних однаково часто зустрічаються два або більше різних числа, його називають відповідно бімодальним або мультимодальним — іншими словами, всі значення, що зустрічаються максимальне число разів, утворюють моди даної множини. У даній статті описано, як знайти моду (моди) безлічі.

Метод1 З 2:

Визначення моди множини чисел

Запишіть числа множини.Моду зазвичай визначають на наборі статистичних даних або безлічі чисельних значень. Таким чином, для знаходження моди вам знадобиться набір чисел. Моду складно визначити в розумі, якщо чисел досить багато, тому в більшості випадків краще записати всі числа або набрати їх на комп'ютері. Якщо у вас є олівець і папір, досить записати всі числа. Якщо ж ви працюєте за комп'ютером, зручніше використовувати Excel.
- Метод визначення моди легше зрозуміти на прикладі. Розглянемо в даному розділі наступний набір чисел:{18, 21, 11, 21, 15, 19, 17, 21, 17}. У наведених нижче кроках ми знайдемо моду цього безлічі.
Розташуйте числа в порядку зростання.після того як ви випишете всі числа, корисно переписати їх в порядку зростання. Хоча можна обійтися і без цього, так знайти моду буде простіше, оскільки однакові числа розташуються поруч. Для великих наборів даних це просто необхідно, так як спроба переглянути Невпорядкований список і підрахувати, скільки разів кожне число з'являється в ньому, досить трудомістка і може привести до помилок.
- Якщо ви використовуєте олівець і папір, Переписування допоможе вам заощадити час в подальшому. Перегляньте числа, знайдіть найменше значення, викресліть його з початкового безлічі і занесіть в новий список. Повторіть те ж саме для другого, потім для третього найменшого числа і так далі, при цьому записуйте кожне число стільки разів, скільки воно зустрічається у вихідному наборі даних.
- Комп'ютер надає більше можливостей-наприклад, в більшості програм для роботи з електронними таблицями можна впорядкувати список значень від найменшого до найбільшого всього лише декількома клацаннями миші.
- У нашому прикладі після впорядкування отримуємо наступну послідовність чисел:{11, 15, 17, 17, 18, 19, 21, 21, 21}.
Підрахуйте, скільки разів повторюється кожне число. після того як ви перепишете значення в порядку зростання, підрахуйте, скільки разів зустрічається кожне число. Пошукайте число, яке найчастіше трапляється в списку. Якщо чисел порівняно небагато і вони розташовані в порядку зростання, це досить просто: знайдіть найбільшу групу однакових значень і підрахуйте, скільки разів вони повторюються.
- Якщо ви використовуєте олівець і папір, спробуйте записати над кожною групою однакових чисел, скільки разів вони повторюються. Якщо Ви користуєтеся комп'ютерною програмою для роботи з електронними таблицями, можна вчинити подібним чином: запишіть результати підрахунків в сусідні осередки або використовуйте одну з опцій для аналізу даних.
- У нашому списку ({11, 15, 17, 17, 18, 19, 21, 21, 21}) 11 і 15 зустрічаються по одному разу, 17 трапляється двічі, 18 і 19 зустрічаються по одному разу, а 21 зустрічається три рази. Таким чином, в даному наборі значень найчастіше зустрічається число 21.
Визначте значення (або значення), які зустрічаються найбільш часто.після того як ви підрахуєте, скільки разів зустрічається кожне число, знайдіть значення, які повторюються найбільшу кількість разів. це і є мода даного безлічі. Пам'ятайте, що Набір чисел може мати не одну, а кілька мод. Якщо в безлічі найбільш часто зустрічаються два числа (тобто вони повторюються однакову кількість разів), таку множину називають бімодальним, якщо три числа — тримодальним і так далі.
- В нашому безлічі ({11, 15, 17, 17, 18, 19, 21, 21, 21}) найбільш часто зустрічається Значення 21, тому21 є модою.
- Якби крім 21 знайшлося ще одне число, якетакож зустрічається три рази, (наприклад, якби безліч включало ще одне число 17), то воно поряд з 21 було б модою.
Не плутайте моду безлічі чисел з його середнім значенням і медіаною.при статистичному аналізі часто розглядають разом такі поняття, як середнє значення, медіана і мода. Їх легко сплутати, так як вони мають схожі назви і іноді їх значення збігаються. Однак незалежно від того, збігається чи ні мода безлічі з його медіаною або середнім значенням, слід пам'ятати, що це три абсолютно різних поняття (дивіться нижче).
- Щоб знайтисереднє значення множини, слід скласти всі числа і поділити на їх кількість. Для нашого прикладу ({11, 15, 17, 17, 18, 19, 21, 21, 21}) середнє значення становить 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160/9 = 17,78. Ми поділили суму значень на 9, оскільки дана множина складається з 9 чисел.
- медіана являє собою "середнє число", яке розділяє менші і більші значення множини на дві рівні половини. Наприклад, для нашого набору значень ({11, 15, 17, 17, 18, 19, 21, 21, 21}) медіаною є число 18, так як зліва і праворуч від нього стоїть по чотири числа. Врахуйте, що якщо множина містить парну кількість чисел, вона не має єдиної медіани. В цьому випадку медіаною зазвичай вважають середнє значення тих двох чисел, які розташовані посередині.

Метод2 З 2:

Знаходження моди в спеціальних випадках

Множина не має моди, якщо кожне значення зустрічається в ньому однакове число разів.якщо всі значення в даному наборі чисел трапляються однакову кількість разів, то у цієї множини немає моди, оскільки жодне число не зустрічається частіше, ніж будь-яке інше. Наприклад, моди не мають ті безлічі, в які кожне число входить по одному разу. Це ж стосується тих множин, в яких кожне число зустрічається двічі, тричі і так далі.
- Якщо ми змінимо набір чисел у нашому прикладі на {11, 15, 17, 18, 19, 21}, так щоб кожне значення зустрічалося лише один раз, то він не матиме моди. Те ж вірно і для безлічі, в якому всі числа зустрічаються двічі, наприклад {11, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21}.
Пам'ятайте, що моду нечислового набору даних можна визначити точно так само, як для числових множин.як правило, більшість наборів даних є "кількісними", тобто містять дані у вигляді чисел. Проте зустрічаються і такі безлічі, члени яких виражені не у вигляді чисел. У таких випадках можна сказати, що» мода " — це те значення, яке зустрічається найчастіше в наборі даних (як і для числових множин).^{[1]X
Джерело інформації} при цьому визначити моду буде можливо, в той час як медіану або середнє значення — не можна.
- Припустимо, при огляді невеликої ділянки землі визначили вид кожного зростаючого на ньому дерева. Вийшов наступний список: {кедр, вільха, кедр, сосна, кедр, кедр, Вільха, Вільха, сосна, кедр}. Такий набір даних називаютьномінальним, оскільки входять до нього члени являють собою назви. В цьому випадку модою є кедр, так як дане слово зустрічається частіше за інших (п'ять разів), в той час як вільха і сосна зустрічаються відповідно три і два рази.
- В розглянутому вище прикладі неможливо знайти середнє значення і медіану, так як набір даних містить Не числа, а назви.
При одномодальному симетричному розподілі мода, середнє значення і медіана збігаються. як зазначалося вище, в деяких випадках мода, медіана і/або середнє значення можуть збігатися. Зокрема, якщо щільність розподілу того чи іншого набору даних утворює ідеально симетричну криву з однією модою (наприклад, гауссіану або дзвоноподібну криву), мода, середнє значення і медіана рівні один одному. Щільність розподілу відображає відносну частоту певних значень, тому мода буде знаходитися точно посередині симетричної кривої розподілу, так як ця найвища точка на графіку відповідає найбільш поширеному значенню. Оскільки набір даних симетричний, ця точка на графіку буде відповідати також медіані (центральній точці в наборі даних) і середньому значенню.
- Як приклад розглянемо набір чисел {1, 2, 2, 3, 3, 3, 4, 4, 5}. Якщо ми відкладемо ці значення на графіку, то отримаємо симетричну криву, яка досягає максимальної висоти 3 при x = 3 і опускається до 1 при x = 1 І x = 5. Значення 3 зустрічається найчастіше, тому воно є модою. Так як 3 розташоване в центрі і по обидві сторони від нього знаходиться чотири числа, воно є такожМедіаною. І нарешті, середнє значення даної множини становить 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3, тобто число 3 є також середнім значенням.
- Виняток з цього правила становлять симетричні безлічі з більш ніж однією модою-вони мають по одній медіані і середньому значенню, з якими не збігаються кілька мод.